|
تضامنًا مع حق الشعب الفلسطيني |
هيكل النواة الذرية
تحوي هذه المقالة أو هذا القسم ترجمة آلية. (مارس 2022) |
هذه مقالة غير مراجعة. (مارس 2022) |
يعد فهم بنية النواة الذرية أحد التحديات المركزية في الفيزياء النووية.
نماذج
نموذج قطرة السائل
نموذج قطرة السائل هو أحد النماذج الأولى من الهيكل النووي، تم اقتراحه من قبل كارل فريدريش فون فايز أوشكر في عام 1935.[1] ويصف النواة بأنها سائل شبه كلاسيكي يتكون من النيوترونات والبروتونات، مع قوة إلكتروستاتيكية طاردة داخلية تتناسب مع عدد البروتونات. تظهر الطبيعة الميكانيكية الكمومية لهذه الجسيمات من خلال مبدأ استبعاد باولي، الذي ينص على أنه لا يمكن أن تكون نواتان من نفس النوع في نفس الحالة. وبالتالي فإن السائل هو في الواقع ما يعرف بسائل فيرمي. في هذا النموذج، تكون طاقة الربط للنواة مع البروتونات و النيوترونات تعطى بواسطة
هو العدد الإجمالي من النيوكليونات (العدد الكتلي). الشروط المتناسبة مع و تمثل حجم وسطح الطاقة من قطرة السائل، وهو مصطلح يتناسب مع يمثل الطاقة الكهروستاتيكية، وهو مصطلح يتناسب مع يمثل مبدأ استبعاد باولي والفصل الأخير هو مصطلح الاقتران، الذي يقلل من الطاقة لأعداد زوجية من البروتونات أو النيوترونات. المعاملات وقد يتم تقدير قوة مصطلح الاقتران نظريًا أو ملاءمته للبيانات. يعيد هذا النموذج البسيط إنتاج السمات الرئيسية للطاقة الرابطة للنواة.
لا يزال افتراض النواة كقطرة من سائل فيرمي مستخدمًا على نطاق واسع في شكل نموذج القطرات المحدودة المدى (FRDM)، بسبب التكاثر الجيد المحتمل لطاقة الربط النووية على الرسم البياني بأكمله، مع الدقة اللازمة للتنبؤ بنواة غير معروفة.[2]
نموذج الصدفة
تعبير «نموذج الصدفة» غامض من حيث أنه يشير إلى حقبتين مختلفتين في حالة الفن. تم استخدامه سابقًا لوصف وجود قذائف نيوكليونية في النواة وفقًا لمقاربة أقرب إلى ما يسمى الآن نظرية المجال المتوسط. في الوقت الحاضر، يشير إلى شكليات مماثلة لشكلية تفاعل التكوين المستخدمة في كيمياء الكم. سوف نقدم الأخير هنا.
مقدمة لمفهوم الصدفة
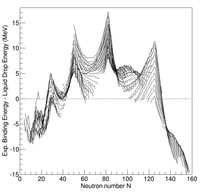
تُظهر القياسات المنهجية للطاقة الرابطة للنواة الذرية انحرافات منهجية فيما يتعلق بتلك المقدرة من نموذج القطرة السائلة. على وجه الخصوص، ترتبط بعض النوى التي لها قيم معينة لعدد البروتونات و / أو النيوترونات ببعضها البعض بإحكام أكثر مما توقعه نموذج القطرة السائلة. تسمى هذه النوى بالسحر الفردي / المزدوج. قادت هذه الملاحظة العلماء إلى افتراض وجود بنية غلاف من النيوكليونات (البروتونات والنيوترونات) داخل النواة، مثل تلك الموجودة في الإلكترونات داخل الذرات.
في الواقع، النيوكليونات هي أشياء كمومية. بالمعنى الدقيق للكلمة، لا ينبغي للمرء أن يتحدث عن طاقات النيوكليونات الفردية، لأنها كلها مرتبطة ببعضها البعض. ومع ذلك، كتقريب يمكن للمرء أن يتصور نواة متوسطة، تنتشر فيها النوى بشكل فردي. نظرًا لطابعها الكمومي، فإنها قد تشغل فقط مستويات طاقة منفصلة. هذه المستويات ليست موزعة بشكل موحد بأي حال من الأحوال؛ بعض فترات الطاقة مزدحمة، وبعضها فارغ، مما يولد فجوة في الطاقات الممكنة. القشرة هي مجموعة من المستويات مفصولة عن المستويات الأخرى بفجوة فارغة واسعة.
تم العثور على مستويات الطاقة من خلال حل معادلة شرودنغر لنوكلون واحد يتحرك في متوسط الجهد الناتج عن جميع النيوكليونات الأخرى. قد يكون كل مستوى مشغولاً بنوكلون، أو فارغًا. بعض المستويات تستوعب عدة حالات كمومية مختلفة بنفس الطاقة؛ يقال إنهم منحطون. يحدث هذا بشكل خاص إذا كان للنواة المتوسطة بعض التناظر.
يسمح مفهوم الأصداف للفرد بفهم سبب ارتباط بعض النوى بإحكام أكثر من غيرها. وذلك لأن نوتين من نفس النوع لا يمكن أن يكونا في نفس الحالة (مبدأ استبعاد باولي). لذا فإن الحالة الأقل طاقة للنواة هي الحالة التي تملأ فيها النوكليونات جميع مستويات الطاقة من الأسفل إلى الأعلى إلى مستوى ما. النواة ذات الأصداف الكاملة مستقرة بشكل استثنائي، كما سيتم شرحه.
كما هو الحال مع الإلكترونات في نموذج غلاف الإلكترون، فإن البروتونات الموجودة في الغلاف الخارجي تكون غير مرتبطة نسبيًا بالنواة إذا كان هناك عدد قليل فقط من البروتونات في تلك الغلاف، لأنها أبعد ما يكون عن مركز النواة. لذلك، فإن النوى التي لها غلاف بروتون خارجي كامل ستكون أكثر إحكامًا ولها طاقة ارتباط أعلى من النوى الأخرى التي تحتوي على عدد إجمالي مماثل من البروتونات. هذا صحيح أيضًا بالنسبة للنيوترونات.
علاوة على ذلك، فإن الطاقة اللازمة لإثارة النواة (أي نقل نواة إلى مستوى أعلى لم يكن مشغولاً من قبل) عالية بشكل استثنائي في هذه النوى. عندما يكون هذا المستوى غير المشغول هو التالي بعد الغلاف الكامل، فإن الطريقة الوحيدة لإثارة النواة هي رفع نواة واحدة عبر الفجوة، وبالتالي إنفاق قدر كبير من الطاقة. خلاف ذلك، إذا كان أعلى مستوى من الطاقة المشغولة يقع في غلاف مملوء جزئيًا، فستكون هناك حاجة إلى طاقة أقل بكثير لرفع النوكليون إلى حالة أعلى في نفس الغلاف.
من المتوقع حدوث بعض التطور في بنية الغلاف التي لوحظت في النوى المستقرة بعيدًا عن وادي الاستقرار. على سبيل المثال، أظهرت ملاحظات النظائر غير المستقرة حدوث تحول وحتى إعادة ترتيب لمستويات الجسيمات المفردة التي يتكون منها هيكل الغلاف.[3] يُلاحظ هذا أحيانًا على أنه إنشاء جزيرة انعكاس أو في تقليل فجوات طاقة الإثارة فوق الأرقام السحرية التقليدية.
الفرضيات الأساسية
يتم وضع بعض الفرضيات الأساسية من أجل إعطاء إطار مفاهيمي دقيق لنموذج الصدفة:
- النواة الذرية هي الكم n- نظام الجسم.
- الحركة الداخلية للنيوكليونات داخل النواة غير نسبية، وسلوكها محكوم بـ معادلة شر-دينجر.
- تعتبر النيوكليونات شبيهة بالنقاط، بدون أي بنية داخلية.
وصف موجز للشكليات
العملية العامة المستخدمة في حسابات نموذج الصدفة هي التالية. أولا يتم تحديد هاميلتوني للنواة. عادة، من أجل التطبيق العملي الحسابي، يتم أخذ المصطلحات المكونة من جسم واحد واثنين فقط في الاعتبار في هذا التعريف. يعتبر التفاعل نظرية فعالة: فهو يحتوي على معلمات مجانية يجب أن تكون مزودة ببيانات تجريبية.
تتمثل الخطوة التالية في تحديد أساس حالات الجسيم الفردي، أي مجموعة من الدالات الموجية التي تصف جميع حالات النكليون الممكنة. في معظم الأحيان، يتم الحصول على هذا الأساس عن طريق حساب هارتري-فوك. مع هذه المجموعة من حالات الجسيم الواحد، تُبنى محددات سلاتر، أي الدوال الموجية لمتغيرات البروتون Z أو متغيرات النيوترون N ، وهي منتجات غير متناظرة لوظائف موجية أحادية الجسيم (غير متماثل بمعنى أنه في ظل تبادل المتغيرات لأي زوج من النيوكليونات، الدالة الموجية تغير فقط الإشارة).
من حيث المبدأ، فإن عدد الحالات الكمومية المتاحة لنواة واحدة عند طاقة محدودة هو عدد محدود، على سبيل المثال n. يجب أن يكون عدد النوكليونات في النواة أصغر من عدد الحالات المتاحة، وإلا فإن النواة لا يمكنها الاحتفاظ بجميع نيوكليوناتها. وإلا فإن النواة لا يمكنها الاحتفاظ بجميع نوياتها. وبالتالي هناك عدة طرق للاختيار Z (أو N) الدول بين n ممكن. في الرياضيات الاندماجية، عدد اختيارات Z الأشياء بين n هو معامل ذي الحدين C
n. إذا n أكبر بكثير من Z (أو N)، وهذا يزيد تقريبا مثل nZ. عمليا، يصبح هذا الرقم كبيرا جدا بحيث يكون كل حساب مستحيلا A=N+Z أكبر من 8.
لتجنب هذه الصعوبة، يتم تقسيم مساحة حالات الجسيم المفرد المحتملة إلى جوهر وتكافؤ، عن طريق القياس مع الكيمياء (انظر جوهر الإلكترون وإلكترون التكافؤ). النواة عبارة عن مجموعة من الجسيمات المفردة التي يُفترض أنها غير نشطة، بمعنى أنها حالات أقل طاقة مرتبطة جيدًا، ولا داعي لإعادة فحص وضعها. لا تظهر في محددات سلاتر، على عكس الحالات الموجودة في فضاء التكافؤ، والذي يمثل مساحة جميع حالات الجسيم الفردي غير الموجودة في القلب، ولكن من المحتمل أن يتم أخذها في الاعتبار عند اختيار بناء (Z-) N- الجسم الموجي. تحدد مجموعة جميع محددات سلاتر الممكنة في فضاء التكافؤ أ الأساس ل (Z-) N- دول الجسم.
تتمثل الخطوة الأخيرة في حساب مصفوفة هاميلتوني ضمن هذا الأساس، وتقطيرها. على الرغم من تقليل أبعاد الأساس بسبب تثبيت اللب، فإن المصفوفات المراد قطرها تصل بسهولة إلى أبعاد تصل إلى 109، وتطلب تقنيات الأقطار المحددة.
تعطي حسابات نموذج الصدفة بشكل عام توافقًا ممتازًا مع البيانات التجريبية. لكنهم يعتمدون بشدة على عاملين رئيسيين:
- طريقة تقسيم الفضاء أحادي الجسيم إلى جوهر وتكافؤ.
- التفاعل الفعال بين النوكليون والنوكليون.
نظريات المجال المتوسط
نموذج الجسيمات المستقلة (إيب)
التفاعل بين النيوكليونات، والذي هو نتيجة للتفاعلات القوية ويربط النوى داخل النواة، يُظهر السلوك الغريب المتمثل في وجود نطاق محدود: فهو يتلاشى عندما تصبح المسافة بين نيوكليونات كبيرة جدًا؛ إنه جذاب على المدى المتوسط ومثير للاشمئزاز في نطاق صغير جدًا. ترتبط هذه الخاصية الأخيرة بمبدأ استبعاد باولي الذي وفقًا له لا يمكن أن يكون فرميونان (النوكليونات هي الفرميونات) في نفس الحالة الكمية. ينتج عن هذا مسار حر متوسط كبير جدًا متوقع لنواة داخل النواة.[4]
الفكرة الرئيسية لنهج الجسيمات المستقلة هي أن النواة تتحرك داخل بئر محتملة معينة (مما يبقيها مرتبطة بالنواة) بشكل مستقل عن النكليونات الأخرى. هذا يرقى إلى استبدال مشكلة الجسم N (تتفاعل الجسيمات N) بمشاكل الجسم الواحد N. هذا التبسيط الأساسي للمشكلة هو حجر الزاوية في نظريات المجال المتوسط. تستخدم هذه أيضًا على نطاق واسع في الفيزياء الذرية، حيث تتحرك الإلكترونات في مجال متوسط بسبب النواة المركزية وسحابة الإلكترون نفسها.
نموذج الجسيمات المستقل ونظريات المجال المتوسط (سنرى أن هناك العديد من المتغيرات) لها نجاح كبير في وصف خصائص النواة بدءًا من تفاعل فعال أو إمكانات فعالة، وبالتالي فهي جزء أساسي من نظرية النواة الذرية. يجب أن يلاحظ المرء أيضًا أنها معيارية بدرجة كافية، من حيث أنه من السهل جدًا توسيع النموذج لإدخال تأثيرات مثل الاقتران النووي، أو الحركات الجماعية للنكليون مثل الدوران، أو الاهتزاز، مضيفًا شروط الطاقة المقابلة في الشكلية. هذا يعني أنه في العديد من التمثيلات، يكون الحقل المتوسط مجرد نقطة بداية لوصف أكثر اكتمالاً والذي يقدم الارتباطات التي تعيد إنتاج الخصائص مثل الإثارات الجماعية ونقل النوكليون.[5][6]
القدرة النووية والتفاعل الفعال
جزء كبير من الصعوبات العملية التي تمت مواجهتها في نظريات المجال المتوسط هو تعريف (أو حساب) إمكانات الحقل المتوسط نفسه. يمكن للمرء أن يميز ذلك تقريبًا بين نهجين:
- نهج الظواهر هو تحديد معلمات للإمكانات النووية من خلال وظيفة رياضية مناسبة. تاريخياً، تم تطبيق هذا الإجراء بأكبر قدر من النجاح بواسطة Sven Gösta Nilsson ، الذي استخدم كمحتمل مذبذب توافقي (مشوه). تعتمد أحدث المعلمات على وظائف أكثر واقعية، والتي تعتبر أكثر دقة لتجارب التشتت، على سبيل المثال. على وجه الخصوص يمكن ذكر الشكل المعروف بإمكانيات Woods – Saxon.
- يهدف نهج الاتساق الذاتي أو نهج هارتري–فوك Hartree–Fock إلى استنتاج الإمكانات النووية رياضيًا من تفاعل فعال بين النوكليون والنيكلون. تتضمن هذه التقنية حلًا لمعادلة شرودنغر بطريقة تكرارية، بدءًا من دالة أنساتز الموجية وتحسينها بشكل متنوع، لأن الإمكانات تعتمد هناك على الدوال الموجية التي سيتم تحديدها. تمت كتابة الأخير كمحددات سلاتر.
في حالة مقاربات هارتري–فوك، لا تكمن المشكلة في العثور على الوظيفة الرياضية التي تصف أفضل الإمكانات النووية، ولكن تلك التي تصف أفضل تفاعل بين النكليون والنيكلون. في الواقع، على النقيض من الفيزياء الذرية حيث يُعرف التفاعل (تفاعل كولوم)، فإن تفاعل النوكليون - النوكليون داخل النواة غير معروف تحليليًا.
هناك سببان رئيسيان لهذه الحقيقة. أولاً، يعمل التفاعل القوي بشكل أساسي بين الكواركات المكونة للنكليونات. تفاعل النوكليون مع النوكليون في الفراغ هو مجرد نتيجة لتفاعل الكوارك والكوارك. في حين أن الأخير مفهوم جيدًا في إطار النموذج القياسي عند الطاقات العالية، إلا أنه أكثر تعقيدًا في الطاقات المنخفضة بسبب حبس اللون وحرية التقارب. وبالتالي لا توجد حتى الآن نظرية أساسية تسمح للفرد باستنتاج تفاعل النوكليون والنيكلون من تفاعل الكوارك والكوارك. علاوة على ذلك، حتى لو تم حل هذه المشكلة، فسيظل هناك فرق كبير بين الحالة المثالية (والأبسط من الناحية المفاهيمية) لاثنين من النيوكليونات تتفاعل في الفراغ، وحالة هذه النيوكليونات التي تتفاعل في المادة النووية. وللمضي قدمًا، كان من الضروري ابتكار مفهوم التفاعل الفعال. هذا الأخير هو في الأساس وظيفة رياضية مع العديد من المعلمات التعسفية، والتي يتم تعديلها لتتوافق مع البيانات التجريبية.
معظم التفاعلات الحديثة ذات نطاق صفري، لذا فهي تعمل عندما يكون النوكيونان على اتصال، كما تم تقديمه بواسطة توني سكيرم.[7]
المناهج المتسقة ذاتيا من نوع هارتري-فوك
نقطة البداية هي أ هاميلتون تحتوي على n الطاقة الحركية الشروط والمصطلحات المحتملة.كما ذكرنا سابقًا، فإن إحدى فرضيات نظرية المجال المتوسط هي أن التفاعل بين الجسمين فقط هو الذي يجب أن يؤخذ في الاعتبار. يمثل المصطلح المحتمل لـ هاميلتون جميع التفاعلات الممكنة بين الجسمين في مجموعة n الفرميونات. إنها الفرضية الأولى.
تتمثل الخطوة الثانية في افتراض أن الدالة الموجية للنظام يمكن كتابتها كمحدد سليتر لمدارات الدوران ذات الجسيم الواحد. هذا البيان هو الترجمة الرياضية لنموذج الجسيمات المستقلة. هذه هي الفرضية الثانية.
لا يزال هناك مجال لتحديد مكونات محدد سلاتر، أي، الدوال الموجية الفردية للنيوكليونات. تحقيقا لهذه الغاية، من المفترض أن إجمالي دالة الموجة (محدد سلاتر) هو أن الطاقة هي الحد الأدنى. هذه هي الفرضية الثالثة.
من الناحية الفنية، فهذا يعني أنه يجب على المرء أن يحسب القيمة المتوسطة لـ (المعروف) ذو الجسمين هاميلتونيان على محدد سلاتر (غير معروف)، ويفرض أن الاختلاف الرياضي الخاص به يختفي. يؤدي هذا إلى مجموعة من المعادلات حيث المجهول هو الدوال الموجية الفردية: معادلات هارتري-فوك. يعطي حل هذه المعادلات الدوال الموجية ومستويات الطاقة الفردية للنكليونات، وبالتالي الطاقة الإجمالية للنواة ودالتها الموجية.
يوضح هذا الحساب المختصر لطريقة هارتري-فوك سبب تسميتها أيضًا بالنهج المتغير. في بداية الحساب، الطاقة الإجمالية هي «دالة لوظائف الموجة الفردية» (ما يسمى الوظيفية)، وبعد ذلك يتم عمل كل شيء من أجل تحسين اختيار هذه الدوال الموجية بحيث يكون للوظيفة حد أدنى - نأمل مطلقة وليست محلية فقط. لكي نكون أكثر دقة، يجب أن نذكر أن الطاقة هي دالة للكثافة، تُعرّف على أنها مجموع الدوال الموجية التربيعية الفردية. تُستخدم طريقة هارتري-فوك أيضًا في الفيزياء الذرية وفيزياء المادة المكثفة كنظرية الكثافة الوظيفية، DFT.
لا يمكن أن تكون عملية حل معادلات هارتري-فوك إلا تكرارية، حيث إنها في الحقيقة معادلة شرودنجر حيث تعتمد الإمكانية على الكثافة، أي بالتحديد على الدوال الموجية المراد تحديدها. من الناحية العملية، تبدأ الخوارزمية بمجموعة من الدوال الموجية الفردية المعقولة بشكل إجمالي (بشكل عام الوظائف الذاتية لمذبذب توافقي). هذه تسمح بحساب الكثافة، ومن ثم إمكانية هارتري-فوك. بمجرد الانتهاء من ذلك، يتم حل معادلة شرودنغر من جديد، وهكذا. يتوقف الحساب - الوصول إلى التقارب - عندما يكون الفرق بين وظائف الموجة، أو مستويات الطاقة، لتكرارين متتاليين أقل من قيمة ثابتة. ثم يتم تحديد متوسط جهد المجال تمامًا، وتصبح معادلات هارتري-فوك معادلات شرودنغر القياسية. ثم يُطلق على هاملتونيان المقابل اسم هارتري-فوك هاملتونيان.
النهج النسبية المتوسطة الميدانية
وُلدت النماذج النسبية للنواة لأول مرة في السبعينيات من القرن الماضي مع أعمال جون ديرك واليكا حول الديناميكا الكمومية، وشحذت النماذج النسبية للنواة في نهاية الثمانينيات من قبل بي.رينج وزملائه في العمل. نقطة البداية لهذه الأساليب هي نظرية المجال الكمي النسبي. في هذا السياق، تحدث تفاعلات النكليون عبر تبادل جسيمات افتراضية تسمى الميزونات. الفكرة، في الخطوة الأولى، هي بناء لاغرانج يحتوي على شروط التفاعل هذه. ثانيًا، من خلال تطبيق مبدأ الفعل الأقل، يحصل المرء على مجموعة من معادلات الحركة. الجسيمات الحقيقية (هنا النيوكليونات) تخضع لمعادلة ديراك ، بينما الجسيمات الافتراضية (هنا الميزونات) تخضع لمعادلات كلاين-جوردون.
في ضوء الطبيعة غير المضطربة للتفاعل القوي ، وأيضًا في ضوء حقيقة أن الشكل المحتمل الدقيق لهذا التفاعل بين مجموعات النيوكليونات معروف بشكل سيئ نسبيًا ، فإن استخدام مثل هذا النهج في حالة النوى الذرية يتطلب جذريًا تقريبية. يتمثل التبسيط الرئيسي في استبدال جميع المصطلحات الميدانية (وهي عوامل بالمعنى الرياضي) في المعادلات بقيمتها المتوسطة (وهي وظائف). بهذه الطريقة ، يحصل المرء على نظام من المعادلات التكاملية التفاضلية المقترنة ، والتي يمكن حلها عدديًا ، إن لم يكن تحليليًا.
نموذج البوزون المتفاعل
نموذج البوزونات المتفاعلة (IBM) هو نموذج في الفيزياء النووية يتم فيه تمثيل النيوكليونات كأزواج ، كل منها يعمل كجسيم بوزون ، مع دوران لا يتجزأ من 0 أو 2 أو 4. وهذا يجعل الحسابات مجدية للنواة الأكبر. هناك عدة فروع لهذا النموذج - في أحدها (IBM-1) يمكن للمرء أن يجمع جميع أنواع النوكليونات في أزواج ، وفي حالات أخرى (على سبيل المثال - IBM-2) يعتبر المرء البروتونات والنيوترونات في أزواج بشكل منفصل.
كسر تلقائي للتماثل في الفيزياء النووية
التناظر هو أحد النقاط المحورية في الفيزياء. تفاعل النوكليون - النوكليون وجميع التفاعلات الفعالة المستخدمة في الممارسة لها تناظرات معينة. إنها ثابتة عن طريق الترجمة (تغيير الإطار المرجعي بحيث لا يتم تغيير الاتجاهات)، عن طريق الدوران (قلب الإطار المرجعي حول بعض المحاور)، أو التكافؤ (تغيير الإحساس بالمحاور) بمعنى أن التفاعل لا يتغير تحت أي من هذه العمليات. ومع ذلك ، في نهج هارتري-فوك ، يمكن أن تظهر الحلول التي ليست ثابتة في ظل مثل هذا التناظر. ثم يتحدث المرء عن كسر التناظر العفوي.
من الناحية النوعية ، يمكن تفسير حالات كسر التناظر العفوي بالطريقة التالية: في نظرية المجال المتوسط ، توصف النواة بأنها مجموعة من الجسيمات المستقلة. يتم إهمال معظم الارتباطات الإضافية بين النيوكليونات التي لا تدخل الحقل المتوسط. ومع ذلك ، يمكن أن تظهر من خلال كسر تناظر الحقل المتوسط هاميلتون، وهو تقريبي فقط. إذا كانت الكثافة المستخدمة لبدء تكرارات عملية هارتري-فوك تكسر بعض التناظرات ، فقد يكسر هارتري-فوك هاميلتون النهائي هذه التماثلات ، إذا كان من المفيد إبقاء هذه التماثلات مكسورة من وجهة نظر الطاقة الإجمالية.
قد تتقارب أيضًا نحو حل متماثل. على أي حال ، إذا كسر الحل النهائي التناظر ، على سبيل المثال ، التناظر الدوراني ، بحيث تبدو النواة ليست كروية ، بل بيضاوية ، فإن جميع التكوينات المستخلصة من هذه النواة المشوهة عن طريق الدوران هي حلول جيدة لهارتري - مشكلة فوك. ثم تتدهور الحالة الأساسية للنواة.
تحدث ظاهرة مماثلة مع الاقتران النووي ، مما ينتهك الحفاظ على عدد الباريونات (انظر أدناه).
امتدادات نظريات المجال المتوسط
ظاهرة الاقتران النووي
الامتداد الأكثر شيوعًا لنظرية المجال المتوسط هو الاقتران النووي. النوى التي تحتوي على عدد زوجي من النوكليونات تكون مرتبطة بشكل منهجي أكثر من النوى ذات العدد الفردي. هذا يعني أن كل نيوكليون يرتبط بآخر ليشكل زوجًا ، وبالتالي لا يمكن وصف النظام بأنه جسيمات مستقلة تخضع لحقل متوسط مشترك. عندما تحتوي النواة على عدد زوجي من البروتونات والنيوترونات ، تجد كل واحدة منها شريكًا لها. لإثارة مثل هذا النظام ، يجب على المرء على الأقل استخدام مثل هذه الطاقة لكسر الزوج. على العكس من ذلك ، في حالة وجود عدد فردي من البروتونات أو النيوترونات ، يوجد نواة غير متزاوجة ، والتي تحتاج إلى طاقة أقل لتحفيزها.
هذه الظاهرة مشابهة بشكل وثيق لتلك الموجودة في النوع 1 الموصلية الفائقة في فيزياء الحالة الصلبة. تم اقتراح أول وصف نظري للاقتران النووي في نهاية عام 1950 من قبل آج بور، بن موتيلسون، وديفيد باينز (التي ساهمت في استقبال جائزة نوبل في الفيزياء في عام 1975 من قبل بور وموتيلسون).[8] كانت قريبة من نظرية بكس لباردين وكوبر وشريففر ، والتي تمثل الموصلية الفائقة للمعادن. من الناحية النظرية ، تتحد ظاهرة الاقتران كما وصفتها نظرية BCS مع نظرية المجال المتوسط: تخضع النيوكليونات لمتوسط إمكانات المجال وللتفاعل الاقتراني.
ال هارتري فوك بوغوليوبوف (هفب) الأسلوب هو نهج أكثر تطورا، [9] مما يمكّن المرء من النظر في الاقتران والتفاعلات الميدانية المتوسطة باستمرار على قدم المساواة. يعتبر HFB الآن المعيار الواقعي في متوسط المعالجة الميدانية للأنظمة النووية.
استعادة التماثل
خصوصية الطرق الميدانية المتوسطة هي حساب الملكية النووية عن طريق كسر التماثل الصريح. إن حساب الحقل المتوسط بأساليب متسقة ذاتيًا (مثل هارتري-فوك)، وتكسر التناظر الدوراني ، وحساب خاصية الاقتران يكسر رقم الجسيمات.
تم تطوير العديد من التقنيات لاستعادة التناظر من خلال الإسقاط على أرقام كمية جيدة.[10]
اقتران اهتزاز الجسيمات
تعد طرق المجال المتوسطة (التي تفكر في النهاية في استعادة التناظر) تقريبًا جيدًا للحالة الأرضية للنظام ، حتى أنها تفترض نظامًا من الجسيمات المستقلة. تأخذ تصحيحات الرتبة الأعلى في الاعتبار حقيقة أن الجسيمات تتفاعل معًا عن طريق الارتباط. يمكن تقديم هذه الارتباطات مع الأخذ في الاعتبار اقتران درجات الحرية الجسيمية المستقلة ، والإثارة الجماعية منخفضة الطاقة للأنظمة مع عدد زوجي من البروتونات والنيوترونات.
وبهذه الطريقة ، يمكن إعادة إنتاج الحالات المثارة عن طريق تقريب الطور العشوائي (RPA) ، وكذلك في النهاية حساب التصحيحات للحالة الأرضية (على سبيل المثال عن طريق نظرية المجال النووي[6]).
انظر أيضًا
- لحظة مغناطيسية نووية
- شاريسا، تعاون أبحاث البنية النووية
مزيد من القراءة
الجمهور العام
- جيمس م. كورك ; مشع physique & اللياقة البدنية النوويةé، دونود (1949).
النصوص التمهيدية
- لوك فالنتين ; لوموند سوباتوميك-ديس كواركس أو سينتراليزس النووية، هيرمان (1986).
- لوك فالنتين ; نويو إت الجسيمات-مود إركليس إت سيم أوكتريز، هيرمان (1997).
- ديفيد هاليداي ; الفيزياء النووية التمهيدية، وايلي وأولاده (1957).
- كينيث كرين ; الفيزياء النووية التمهيدية، وايلي وأولاده (1987).
- كارلوس بيرتولاني ; الفيزياء النووية باختصار، مطبعة جامعة برينستون (2007).
النصوص الأساسية
- بيتر إي هودجسون; التفاعلات النووية والبنية النووية. مطبعة جامعة أكسفورد (1971).
- ايرفينغ كابلان; الفيزياء النووية، سلسلة أديسون ويسلي في العلوم والهندسة النووية ، أديسون ويسلي (1956). الطبعة 2 (1962).
- أ. بور & ب. موتيلسون ; الهيكل النووي, 2 المجلد. بنيامين (1969-1975). المجلد 1 : حركة الجسيمات واحدة ؛ المجلد 2 : التشوهات النووية. شركة بار العالمية للنشر العلمي (1998), (ردمك 981-02-3197-0).
- بي رينج آند بي شوك; مشكلة العديد من الأجسام النووية, سبرينغر فيرلاغ (1980), (ردمك 3-540-21206-X)
- أ. دي شاليت وهـ. فيشباخ; الفيزياء النووية النظرية, 2 المجلد. جون وايلي وأولاده (1974). المجلد 1: الهيكل النووي؛ المجلد 2: التفاعلات النووية, (ردمك 0-471-20385-8)
المراجع
- ^ von Weizsäcker, C. F. (1935). "Zur Theorie der Kernmassen". Zeitschrift für Physik (بDeutsch). 96 (7–8): 431–458. Bibcode:1935ZPhy...96..431W. DOI:10.1007/BF01337700.
- ^ Moeller، P.؛ Myers، W. D.؛ Swiatecki، W. J.؛ Treiner، J. (3 سبتمبر 1984). "Finite Range Droplet Model". Conference: 7. International Conference on Atomic Masses and Fundamental Constants (AMCO-7), Darmstadt-Seeheim, F.R. Germany. OSTI:6441187.
- ^ Sorlin، O.؛ Porquet، M.-G. (2008). "Nuclear magic numbers: New features far from stability". Progress in Particle and Nuclear Physics. ج. 61 ع. 2: 602–673. arXiv:0805.2561. Bibcode:2008PrPNP..61..602S. DOI:10.1016/j.ppnp.2008.05.001.
- ^ Brink، David؛ Broglia، Ricardo A. (2005). Nuclear Superfluidity. Cambridge University Press. ISBN:9781139443074. مؤرشف من الأصل في 2022-03-14.
- ^ Ring، P.؛ Schuck، P. (1980). The nuclear many-body problem. Springer Verlag. ISBN:978-3-540-21206-5.
- ^ أ ب Idini، A.؛ Potel، G.؛ Barranco، F.؛ Vigezzi، E.؛ Broglia، R. A. (2015). "Interweaving of elementary modes of excitation in superfluid nuclei through particle-vibration coupling: Quantitative account of the variety of nuclear structure observables". Physical Review C. ج. 92 ع. 3: 031304. arXiv:1504.05335. Bibcode:2015PhRvC..92c1304I. DOI:10.1103/PhysRevC.92.031304.
- ^ Beiner، M.؛ Flocard، H.؛ Van Giai، Nguyen؛ Quentin، P. (1975). "Nuclear ground-state properties and self-consistent calculations with the skyrme interaction". Nuclear Physics A. ج. 238: 29–69. Bibcode:1975NuPhA.238...29B. DOI:10.1016/0375-9474(75)90338-3.
- ^ Broglia، Ricardo A.؛ Zelevinsky، Vladimir (2013). Fifty Years of Nuclear BCS: Pairing in Finite Systems. World Scientific. DOI:10.1142/8526. ISBN:978-981-4412-48-3.
- ^ "Hartree-Fock-Bogoliubov Method". مؤرشف من الأصل في 2018-08-31.
- ^ Bayman، B. F. (1960). "A derivation of the pairing-correlation method". Nucl. Phys. ج. 15: 33–38. Bibcode:1960NucPh..15...33B. DOI:10.1016/0029-5582(60)90279-0.
روابط خارجية
- العربية
- باللغة الإنجليزية Institut de Physique Nucléaire (IPN), France
- باللغة الإنجليزية Facility for Antiproton and Ion Research (FAIR), Germany
- باللغة الإنجليزية Gesellschaft für Schwerionenforschung (GSI), Germany
- باللغة الإنجليزية Joint Institute for Nuclear Research (JINR), Russia
- باللغة الإنجليزية Argonne National Laboratory (ANL), USA
- باللغة الإنجليزية Riken, Japan
- باللغة الإنجليزية National Superconducting Cyclotron Laboratory, Michigan State University, USA
- باللغة الإنجليزية Facility for Rare Isotope Beams, Michigan State University, USA
- الفرنسية
- باللغة الفرنسية معهد اللياقة البدنية ، فرنسا
- باللغة الفرنسية مركز الطيف الطيفي النووي والطيف الطيفي الجماعي ، فرنسا
- باللغة الفرنسية خدمة اللياقة البدنية النوية إرمير سي / دام ، فرنسا
- باللغة الفرنسية المعهد الوطني للجسيمات البدنية (في2ص3)، فرنسا
- باللغة الفرنسية غراند أسك أوكلراتورز ناشيونال دي أوف لوردز (غانيل)، فرنسا
- باللغة الفرنسية مفوضية-لينيرجي أتوميك ، فرنسا
- باللغة الفرنسية المركز الأوروبي للبحوث النووية ، سويسرا
 المخطط المباشر للنويدات-الوكالة الدولية للطاقة الذرية
المخطط المباشر للنويدات-الوكالة الدولية للطاقة الذرية
| هيكل النواة الذرية في المشاريع الشقيقة: | |