نظرية القشرة الكروية

في الميكانيكا الكلاسيكية، تبسط نظرية القشرة الكروية أو نظرية سطح الكرة الجوفاء الحسابات المتعلقة بالجاذبية بشكل يمكن تطبيقه على الأجسام داخل وخارج جسم متناظر كرويًّا. لهذه النظرية تطبيقات محددة في علم الفلك.

أثبت إسحاق نيوتن نظرية القشرة وقال:

1. يجذب الجسم المتناظر كرويًّا الأجسام الخارجية كما لو كانت كتلته مركزة في نقطة في مركزه.
2. إذا كان الجسم قشرةً متناظرةً كرويًّا (مثلًا كرة جوفاء)، لا تؤثر القشرة بقوى جذب صافٍ على أي جسم داخلها، مهما يكن موقع الجسم داخلها.

ينتج عن ذلك أن قوة الجذب تتغير خطيًّا مع البعد عن المركز في جسم كروي صلب كثافته ثابتة، لتصبح معدومة بالتناظر في مركز الكتلة (مركز العطالة). يمكن اعتبار هذا كالتالي: لتكن نقطة في كرة كتلك المذكورة، على بعد $r$ من مركز الكرة. يمكن عندها، وفقًا لنظرية القشرة الكروية، إهمال كل السطوح القشرية ذات الأقطار الأكبر. لذا، تتناسب الكتلة المتبقية $m$ مع $r^3$ (لأنها تعتمد على الحجم)، وقوة الجاذبية المطبقة عليها تتناسب مع $m/r^2$ (قانون التربيع العكسي)، فيكون أثر الجاذبية الكلي متناسبًا مع $r^3/r^2=r$، أي مترافقًا خطيًّا مع $r$.

كانت النتائج مهمة لتحليل نيوتن لحركة الكواكب السيارة؛ لم تكن النتائج بديهية، لكن يمكن إثباتها بالحساب التفاضلي. (كبديل، يوفر قانون غاوس للجاذبية طريقةً أبسط بكثير لإثبات النتائج نفسها).

بالإضافة إلى الجاذبية، يمكن استخدام نظرية القشرة الكروية أيضًا لوصف الحقل الكهربائي الذي تولده كثافة شحنة ساكنة متناظرة كرويًّا، أو بشكل مشابه لأي ظاهرة تتبع لقانون التربيع العكسي (التناسب التربيعي العكسي). تركز الاشتقاقات أدناه على الجاذبية، لكن النتائج يمكن تعميمها بسهولة على القوى الكهربائية الساكنة. بل يمكن تعميمها أيضًا على مسائل أجسام القطوع الكروية العامة.

اشتقاق حقل الجاذبية خارج جسم كروي مصمت

هناك ثلاث خطوات لإثبات نظرية نيوتن القشرية. أولًا، نشتق معادلة الحقل الثقالي (أو حقل الجاذبية) لحلقة مادية (ذات كتلة). ثانيًا، بترتيب عدد لا نهائي من الحلقات لا متناهية الرقة لصنع قرص، تُستخدم تلك المعادلة المطبقة على حلقة لدراسة الحقل الثقالي لقرص. أخيرًا، بترتيب عددٍ لا منتهٍ من الأقراص لا متناهية الرقة لصنع كرة، تُستخدم تلك المعادلة المطبقة على قرص لإيجاد حقل الجاذبية الناتج عن كرة.

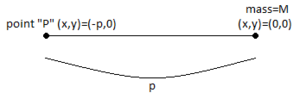
يعطى الحقل الثقالي في نقطة تدعى $P$ عند $(x,y)=(-p,0)$ على محور السينات $x$ الناتج عن نقطة مادية $M$ في مركز الإحداثيات بالعلاقة:

$E_{point}=\frac{GM}{p^2}$

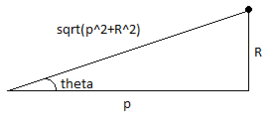
نفترض تحرك هذه الكتلة إلى الأعلى على محور العينات $y$ إلى نقطة $(0,R)$. المسافة بين $P$ والنقطة المادية أصبحت الآن أكبر مما سبق؛ إذ تصبح بطول وتر المثلث ذي الضلعين $P$ و $R$ والذي يساوي $sqrt(p^2+R^2)$

$E_{elevatedpoint}=\frac{GM}{(p^2+R^2)}$

تساوي شدة الحقل الثقالي الذي يمكنه سحب جسيم عند النقطة $P$ باتجاه $x$ إلى حقل الجاذبية مضروبًا بـ $cos\theta$ حيث $\theta$ زاوية مجاورة لمحور السينات $x$. في هذه الحالة، $cos(theta)=p/sqrt(p^2+R^2)$.

$E_x=\frac{GM\cos \theta }{p^2+R^2}$

وتكتب بشكل أبسط:

$E_x=\frac{GMp}{(p^2+R^2{)}^{3/2}}$

لنفترض أن هذه الكتلة موزعة بانتظام على حلقة مركزها مركز الإحداثيات وتقابل النقطة $P$ بنفس نصف القطر $R$. لأن كل الكتلة تقع على نفس الزاوية بالنسبة لمحور السينات $x$، والمسافة بين النقاط الواقعة على الحلقة نفسها المسافة السابقة؛ الحقل الثقالي للحلقة باتجاه $x$ عند نقطة $P$ يساوي الحقل الناتج عن نقطة مادية تقع في نقطة $R$ فوق محور العينات $y$:

$E_{ring}=\frac{GMp}{(p^2+R^2{)}^{3/2}}$

لإيجاد الحقل الثقالي لقرص عند نقطة $P$، يمكن وضع عدد غير منتهٍ من الحلقات لا متناهية الرقة مقابل النقطة $P$، كلًّا بنصف قطر $y$، وعرض $dy$، وكتلة $dM$ داخل بعضها البعض لتشكيل قرص. كتلة أي من الحلقات $dM$ هي كتلة القرص مضروبةً بنسبة مساحة الحلقة $2*pi*y*dy$ إلى المساحة الكلية للقرص $pi*R^2$، إذن: $dM=M*2*y*dy/R^2$.

$dE=\frac{Gp*dM}{(p^2+y^2{)}^{3/2}}$

$\int dE=\int \frac{\frac{2GM}{R^2}*p*y*dy}{(p^2+y^2{)}^{(}3/2)}$

بجمع الآثار الجزئية لكل هذه الحلقات في الحقل الثقالي تنتج علاقة الحقل الثقالي لقرص. يكافئ هذا مكاملة العلاقة السابقة من $y=0$ إلى $y=R$، والنتيجة:

$E_{disc}=\frac{2GM}{R^2}*(1-\frac{p}{sqrt(p^2+R^2)})$

لإيجاد الحقل الثقالي لكرة مركزها مركز الإحداثيات عند نقطة $P$، يمكن وضع عدد غير منتهٍ من الأقراص لا متناهية الرقة المقابلة للنقطة $P$، كل بنصف قطر $R$، وعرض $dx$ وكتلة $dM$ مع بعضها البعض.

تتبع أنصاف أقطار هذه الأقراص $R$ لارتفاع المقطع العرضي من كرة (ذات نصف قطر ثابت $a$)، وهي معادلة نصف دائرة: $R=sqrt(a^2-x^2)$. تتراوح قيمة $x$ بين $-a$ و$a$.

كتلة أي من الأقراص $dM$هي كتلة الكرة $M$ مضروبةً بنسبة حجم قرص لا منتهي الرقة إلى حجم كرة (ذات نصف قطر ثابت $a$). حجم القرص لا متناهي الرقة هو $pi*R^2*dx$ أو $pi*(a^2-x^2)*dx$. إذن: $dM=M*pi*(a^2-x^2)*dx/((4/3)*pi*a^3)$. وبالتبسيط: $dM=M*3*(R^2-x^2)*dx/(4*a^3)$. تتراوح $x$ بين $-a$ و$a$.

يتغير بُعد كل قرص عن النقطة $P$ مع موقعه ضمن «الكرة» المكونة من الأقراص. لذا تجب الاستعاضة عن $p$ بـ $p+x$. تتراوح $x$ بين $-a$ و$a$.

بالاستعاضة عن $M$ بـ $dM$، وعن $R$ بـ $sqrt(a^2-x^2)$، وعن $p$ بـ $p+x$ في معادلة «القرص» ينتج:

$dE=\frac{\frac{2G*(3M*(a^2-x^2))}{4a^3}}{sqrt(a^2-x^2{)}^2}*(1-\frac{p+x}{sqrt((p+x{)}^2+sqrt(a^2-x^2{)}^2))}dx$

بالتبسيط:

$\int dE=\underset{-a}{\overset{a}{\int }}\frac{3GM}{2a^3}*(1-\frac{p+x}{sqrt(p^2+a^2+2px)})dx$

بمكاملة الحقل الناتج عن كل قرص رقيق من $x=-a$ إلى $x=+a$ بالنسبة لـ $x$، وبعد حسابات جبرية دقيقة، تنتج نظرية نيوتن القشرية بشكل جميل.

$E=G*M/p^2$ حيث $p$ هي المسافة بين مركز الكتلة الكروية ونقطة ما $P$. يمكن حساب الحقل الثقالي الناتج عن كتلة كروية باعتبار كل الكتلة جسيمًا نقطيًّا يقع في مركز الكرة.

اشتقاق حقل الجاذبية خارج قشرة كروية

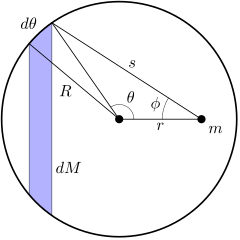
يمكن نمذجة جسم صلب متناظر كرويًّا على أنه عدد غير منته من القشور الكروية متحدة المركز ومتناهية الرقة. إذا أمكن اعتبار إحدى هذه القشور على أنها نقطة مادية، يمكن اعتبار مجموعة قشور (أي الكرة) أيضًا كنقطةً ماديةً. لنأخذ قشرة كهذه (يُظهر الشكل مقطعًا عرضيًّا):

(ملاحظة: dθ الظاهرة في الشكل تعبر عن زاوية صغيرة، وليس طول القوس. طول القوس هو R dθ).

بتطبيق قانون الجذب العام لنيوتن، مجموع القوى الناتجة عن العناصر التفاضلية الكتلية في الجزء المظلل:

$dF=\frac{GmdM}{s^2}.$

لكن، بسبب وجود إلغاء جزئي ناتج عن الطبيعة الشعاعية للقوة مع التناظر الدائري للمقطع الطولي المظلل، تعطى المركبة الشعاعية المتبقية (باتجاه $m$) بالعلاقة:

$d{F}_r=\frac{GmdM}{s^2}\cos \varphi .$

القوة الكلية المؤثرة على $m$، إذن، هي ببساطة مجموع القوة المطبقة من قبل كل المقاطع الطولية المكونة للدائرة. بتقليص عرض كل مقطع طولي، وزيادة عدد المقاطع، يمكن التعبير عن المجموع بالعلاقة التكاملية:

$F_r=\int d{F}_r$

بما أن $G$ و$m$ ثوابت، يمكن إخراجهما من التكامل:

$F_r=Gm\int \frac{dM\cos \varphi }{s^2}.$

لحساب قيمة هذا التكامل، يجب أولًا إيجاد علاقة $dM$ كتابع لـ$d\theta$.

السطح الكلي للقشرة الكروية:

$4\pi R^2$

بينما مساحة سطح الشريحة الرقيقة بين $\theta$ و$\theta +d\theta$:

$2\pi R^2\sin \theta d\theta$

إذا كانت كتلة القشرة $M$، يكون عندها:

$dM=\frac{2\pi R^2\sin \theta }{4\pi R^2}Md\theta =\frac{1}{2}M\sin \theta d\theta$

و

$F_r=\frac{GMm}{2}\int \frac{\sin \theta \cos \varphi }{s^2}d\theta$

بقانون التجيبات (جيب التمام):

$\cos \varphi =\frac{r^2+s^2-R^2}{2rs}$

$\cos \theta =\frac{r^2+R^2-s^2}{2rR}.$

هاتان العلاقتان تربطان بين البارامترات الثلاث: $\theta$ و ϕ و s التي تظهر معًا في التكامل. عند تزايد $\theta$ من 0 إلى $\pi$ راديان، ϕ تتغير من القيمة الابتدائية 0 إلى قيمة أعظمية حتى تعود بالنهاية للصفر عند $\theta =\pi$. أمّا s فتتزايد من قيمتها الابتدائية $r-R$ حتى القيمة النهائية $r+R$ عند تزايد $\theta$ من 0 حتى $\pi$ راديان. ويتوضح هذا بالرسم المتحرك الآتي:

لإيجاد التابع الأصلي للتكامل، علينا جعل s المتغير المستقل للتكامل بدلًا من $\theta$

$\sin \theta d\theta =\frac{s}{rR}ds.$

نحصل على:

$F_r=\frac{GMm}{2rR}\int \frac{\cos \varphi }{s}ds$

إذ يتزايد المتغير الجديد للتكامل s من $r-R$ إلى $r+R$.

بإدخال علاقة ##رمز## باستخدام أولى علاقات «قانون جيب التمام» أعلاه، نحصل على:

$F_r=\frac{GMm}{4r^{2}R}\int (1+\frac{r^2-R^2}{s^2})ds.$

ما يدل على أن قوة الجذب نفسها تلك الناتجة عن النقطة المادية في مركز القشرة ذات الكتلة نفسها.

أخيرًا، بمكاملة كل القشور الكروية متناهية الرقة ذات الكتلة $dM$، يمكننا الحصول على الأثر الكلي لكرة صلبة على جذب جسم خارجها.

$F_{total}=\int d{F}_r=\frac{Gm}{r^2}\int dM.$

يمكن التعبير عن $dM$ كتابع لـ $x$، بين نصفي القطرين $x$ و$x+dx$ أي:

$dM=\frac{4\pi x^{2}dx}{\frac{4}{3}\pi R^3}M=\frac{3M{x}^{2}dx}{R^3}$

بالتالي، تكون الجاذبية الكلية:

$F_{total}=\frac{3GMm}{r^2{R}^3}\underset{0}{\overset{R}{\int }}{x}^{2}dx=\frac{GMm}{r^2}$

ما يدل على إمكانية اعتبار جاذبية جسم كروي مصمت لجسم خارجي على أنها نفسها جاذبية نقطة مادية في مركز الكرة ذات الكتلة نفسها للتبسيط.

اشتقاق حقل الجاذبية داخل قشرة كروية

الفرق، في حالة نقطة داخل قشرة، أنه عندما تكون $\theta$ تساوي الصفر، تأخذ ϕ قيمة $\pi$ راديان وs قيمة $R-r$. عند تزايد $\theta$ من 0 إلى $\pi$ راديان، تتناقص ϕ من القيمة الابتدائية $\pi$ راديان إلى الصفر وتتزايد s من القيمة الابتدائية $R-r$ إلى القيمة $R+r$، كما يتضح من الشكل الآتي:

بإدخال هذه الشروط الحدية إلى التابع الأصلي نحصل على:

$s-\frac{r^2-R^2}{s}$

ونحصل في هذه الحالة على:

$F_r=0$

ما يعني أن قوى الجذب الصافي المؤثرة على النقطة المادية من الكتل العنصرية للقشرة، خارج نقطة القياس، تلغي بعضها بعضًا.

تعميم: إذا كان $f=k/r^p$، تكون القوة المحصلة داخل القشرة:

$F(r)=\frac{GMm}{4r^{2}R}\underset{R-r}{\overset{R+r}{\int }}(\frac{1}{s^{p-2}}+\frac{r^2-R^2}{s^p})ds$

ينتج عن هذا أن $F(r)$ تساوي الصفر تمامًا إذا وفقط إذا كانت $p=2$ خارج القشرة (أي $r>R$ أو $r<-R$):

$F(r)=\frac{GMm}{4r^{2}R}\underset{r-R}{\overset{r+R}{\int }}(\frac{1}{s^{p-2}}+\frac{r^2-R^2}{s^p})ds$

الاشتقاق باستخدام قانون غاوس

نظرية القشرة الكروية هي نتيجة مباشرة لقانون غاوس للجاذبية الذي ينص على أن:

${\int }_S\mathbf{g}\cdot d\mathbf{S}=-4\pi GM$

حيث $M$ هي كتلة الجزء من التوزع الكتلي المتناظر كرويًّا الواقع داخل الكرة ذات نصف القطر $r$

و${\int }_S\mathbf{g}\cdot d\mathbf{S}={\int }_S\mathbf{g}\cdot \hat{\mathbf{n}}dS$ هو التكامل السطحي للحقل الثقالي g على أي سطح مغلق تكون الكتلة الإجمالية ضمنه مساويةً $M$، حيث شعاع الواحدة $\hat{\mathbf{n}}$ هو الناظم الخارجي على السطح.

يجب على الحقل الثقالي لتوزع كتلي متناظر كرويًّا، كذلك الناتج عن نقطة مادية أو قشرة كروية أو كرة متجانسة أيضًا أن يكون متناظرًا كرويًّا. إذا كان $\hat{\mathbf{n}}$ شعاعًا واحديًّا يتجه من مركز التناظر إلى نقطة أخرى في الحقل الثقالي، يجب بالتالي أن يوجد في هذه النقطة:

$\mathbf{g}=g(r)\hat{\mathbf{n}}$

حيث تعتمد قيمة $g(r)$ فقط على البعد $r$ عن مركز التناظر.

باختيار السطح المغلق كرة نصف قطرها $r$ مركزها مركز التناظر، يكون الناظم الخارجي على السطح، $\hat{\mathbf{n}}$، متجهًا بالضبط من مركز التناظر باتجاه التوزع الكتلي.

نحصل بالتالي على:

$\mathbf{g}=g(r)\hat{\mathbf{n}}$

و

${\int }_S\mathbf{g}\cdot d\mathbf{S}=g(r){\int }_{S}dS=g(r)4\pi r^2$

بما أن مساحة سطح الكرة $4\pi r^2$.

ينتج من قانون غاوس:

$g(r)4\pi r^2=-4\pi GM$

أي أن:

$g(r)=-\frac{GM}{r^2}.$