نظرية التعقيد الحسابي

نظرية التعقيد الحسابي

نظرية التعقيد هي فرع من فروع نظرية الحوسبة والرياضيات، وهذه النظرية تتركز في تصنيف المسائل الحاسوبية حسب صعوبتها وربط أقسام التعقيد complexity classes ببعضها، والمسألة الحاسوبية هي المسألة التي يستطيع الحاسوب بحلها.

ويمكن اعتبارها مسألة صعبة إذا استخدمت كمية مُعينة من الموارد أياً كانت الخوارزمية. ولعل النماذج الحسابية هي الطريقة الأمثل في هذه النظرية لدراسة هذه المسائل وتحديد كمية الموارد اللازمة مثل: الوقت أو حجم المكان الإضافي اللازم، وتوجد معايير تعقيد أخرى مثل: الاتصال (مستخدم في نظرية تعقيد الاتصال) وعدد البوابات في الدارات المنطقية (مستخدم في نظرية تعقيد الدارات المنطقية) وكذلك عدد المعالجات (مستخدم في الحساب المتوازي).

وأحد أهم أساسيات نظرية التعقيد الحسابي هي إظهار الحدود العملية لما يستطيع الحاسوب القيام به وما لا يستطيع القيام به.

المجالات القريبة في علم الحاسوب النظري هي تحليل الخوارزميات ونظرية الحاسوبية، والفرق بين تحليل الخوارزميات ونظرية التعقيد الحسابية هو أن الأول يسأل عن خوارزمية معينة لحل مسألة، بينما الآخر يسأل عن كل الخوارزميات التي يمكنها حل المسألة، وبالتحديد فإن الأخير يحاول تصنيف المسائل التي يمكن حلها أو عدم حلها بوضع كمية مُحددة من الموارد، أما وضع الحدود للموارد الموجودة هو ما يميز نظرية التعقيد الحسابي عن النظرية الحاسوبية أي أن النظرية الحاسوبية تسأل عن أية مسائل يمكن حلها بواسطة خوارزمية.

مسائل، مُدخل وطول المُدخل

تعريف المُدخل

بشكل عام مُدخل (instance) لمسألة حاسوبية هو مجموعة معطيات $x_1,\cdots ,x_d$، والمسألة الحاسوبية هي حساب دالة متعلقة بهذه المعطيات.

مثال حساب المُحدد لمصفوفة: المدخلات لهذه المسألة هي القيم في المصفوفة والمُخرج هو المحدد، وقد يُنظر إلى المسألة على أنها مجموعة من المدخلات والمُخرج الملائم للمُدخل، ويمكن أن تكون المدخلات بأطوال مختلفة، وطول المُدخل هو كمية البتات اللازمة لترميز المُدخل بشكل ملائم، أي أن المُدخل يكون سلسلة (string) تابعة ل- $\{0,1{\}}^{*}$، مثال يمكن ترميز العدد بواسطة تمثيله بنظام العد الثنائي (الترميز الملائم للعدد 15 هو 1111)، أما ترميز المخطط فيكون بواسطة القيم في المصفوفة الملائمة له.

لغات أو مسائل التقرير

مسألة التقرير هي نوع خاص من المسائل الحاسوبية التي يكون جوابها إما نعم أو لا، أو 0 و 1، وهذا النوع من المسائل يُعرف أيضا باللغات، في حين أن الأعضاء التابعة لهذه اللغة هي المُدخلات التي جوابها نعم، والهدف يكون بإعطائنا مُدخل يجب التقرير إذا ما هو عضو في هذه اللغة أو لا وذلك بواسطة خوارزمية.

مثال: فلتكن مسألة تقرير إذا كان عدد معطى هو أولي، اللغة هي كل الأعداد الأولية، ولتقرير إذا كان مُدخل معين هو أولي نشغل الخوارزمية التالية: «فحص إذا ما كان العدد المعطى يقبل القسمة على أي عدد من 2 حتى العدد نفسه - ما عدا للعدد نفسه- ، إذا قَبِل (الجواب نعم) فهو ليس أولياً وخلاف ذلك العدد أولي».

مسائل دالة

مسائل دالة (function problem) هي مسائل يكون فيها لكل مُدخل مُخرجٌ وحيد، وتختلف هذه المسائل عن مسائل التقرير في أن مُخرجها قد يكون غير الإجابة بـ (نعم ولا).

مثال تحليل لعوامل أولية حيث يكون المُدخل هو عدد، والمُخرج هو التحليل لعوامل لهذا العدد، وقد يُعتقد أن مسائل الدالة أغنى من مسائل التقرير، ولكن هذا غير صحيح بالضرورة، إذ يمكن تحويل كل مسألة دالة إلى مسألة تقرير، وفي مثال التحليل لعوامل أولية المدخل هو عدد x، وقائمة أعداد x₁,x₂,...,x_d، والمُخرج هو نعم فقط إذا كان حاصل ضرب الأعداد هو x، إضافة إلى أن كل عدد بالقائمة هو أولي.

قياس تعقيد الخوارزمية

لقياس صعوبة مسألة حاسوبية وجب على المرء أن يقيس الوقت اللازم لأفضل خوارزمية كي تحل المسألة، وبشكل عام فالوقت قد يرتبط بطول المُدخل فالمُدخلات الطويلة حتماً ستحتاج وقتاً أطول للوصول إلى الحل. لذا فإن قياس الوقت اللازم لحل مسألة هو دالة مرتبطة بطول المُدخل، وبشكل عام طول المُدخل يكون ب الاثباتات، لذا فإن علم التعقيد بالأساس يبحث مدى قابلية الخوارزمية للتوسع.

فلنفرض أن n هو طول المُدخل، حينها يمكن التعبير عن الوقت اللازم للخوارزمية بواسطة n، وبما أن الوقت اللازم لحل المسألة قد يختلف تبعاً لكل مُدخل فإنه يُؤخذ بالاعتبار تعقيد وقت الحالة الأسوأ (T(n، والذي هو الوقت الأطول الذي ستحتاجه الخوارزمية بالنسبة لكل المدخلات.

إذا كانت (T(n حدودية، أي يوجد ثابت c > 0 بحيث أن (T(n)=O(n^c حينها نصف الخوارزمية بأنها (خوارزمية حدودية الوقت) أي أن وقت الخوارزمية هو وقت حل حدودي. وأطروحة كوبهام تقترح أن أي مسألة يمكن حلها بكمية معقولة من الموارد إذا وجدت خوارزمية تحلها بوقت حدودي.

نماذج حاسوبية ومقاييس التعقيد

نماذج حاسوبية

المقالة الرئيسية: نموذج حوسبة

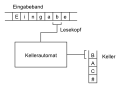
وهي محاكاة نظرية لفكرة الحاسوب أي أن النموذج الحاسوبي هو آلة وهي التي تقوم بعمليات أساسية (قد تختلف من نموذج لآخر)، ونظرية التعقيد تسأل عن مجموعة العمليات الأصغر التي يمكنها حل المسألة، وأكثر النماذج شيوعا في نظرية التعقيد هي آلة تيورنج وهي آلة حاسوبية تعالج رموز مكتوبة على شريط العمليات، وهذا النموذج قد لا يكون عملي ولكن هناك إيمان إذا مسألة ما يمكن حلها بواسطة خوارزمية ما فحينها يمكن حل هذه المسألة بواسطة آلة تيورنج، وهذه الفرضية كانت المقال الأساسي في اطروحة تشيرش-تيورنج، وحسب ما هو معلوم كل ما يمكن حسابهُ بواسطة نماذج أخرى يمكن حسابه كذلك بواسطة آلة تيورنج. ولهذا السبب فان هذه الآلة هي الأكثر شيوعا في نظرية التعقيد.

أكثر النماذج الحاسوبية المستخدمة هي:

• 
  آلة تورنغ
• 
  الة سجل
• 
  الأوتومات غير المنتهي ذو المكدس
• 
  آلة الحالات المحدودة

قياس التعقيد

ولكي يكون قياس التعقيد، والذي هو استخدام كمية مُعينة من الموارد مثل: الوقت أو المكان، دقيقا ومُعرفا بشكل رياضياتى سليم كانت الحاجة للنماذج الحاسوبية مثال: آلة تيورنج، وقد نعرف الوقت اللازم لحل مسألة بواسطة آلة تيورنج،M , مع المدخل للالة،x, هو عدد الخطوات أو التحول من وضعية لوضعية اللازمة للالة حتى التوقف والاتيان بالنتيجة (مثل: نعم أو لا). ونقول أنَّ آلة تيورنج، M , وقت عملها هو (f(n إذا كان الوقت اللازم للالة M على كل مُدخل طولة n هو (f(n . ونقول أنَّ مسألة يمكن حلها بوقت (f(n إذا يوجد آلة تيورنج M الوقت الذي تحتاجه لحل مُدخل طوله n هو (f(n . وبما أنَّ نظرية التعقيد اهتمامها بتصنيف المسائل حسب صعوبتها لذا فالمرئ يمكنه تعريف مجموعة مسائل تحقق معيار مُعين مثال ذلك المجموعة ((DTIME(f(n وهي مجموعة المسائل التي يوجد آلة تيورنج قطعية التي تحلها بوقت (f(n .

هنالك عدة مقاييس للتعقيد ولعل اهمها هو الوقت والمكان، ولعل بديهيات بلم (Blum axioms) في نظرية التعقيد تُعرف هذه المقاييس. مقاييس أخرى مُستخدمة في نظرية التعقيد هي تعقيد الاتصال وتعقيد الدارات المنطقية وتعقيد شجرة التقرير. وبشكل عام في قياس تعقيد الخوارزميات شاع استخدام رمز O الكبير.

تعقيد الحالة الأفضل والحالة الأسوأ وتعقيد الحالة المتوسطة

تعقيد الحالة الأفضل والحالة الأسوأ والمتوسطة هي ثلاث طرق مختلفة لقياس تعقيد الوقت أو (أي مقياس اخر) لمُدخلات مختلفة من نفس الطول، وبما أنه باختلاف المُدخلات قد تكون بعض المُدخلات حلها اسرع من الأخريات لذا نعرف التالي:

• تعقيد الحالة الأفضل: وهو الوقت اللازم لحل مُدخل مسألة حيث أن هذا المُدخل يستلزم اقل وقت من بين كل المُدخلات المحتملة التي لها نفس الطول.
• تعقيد الحالة الأسوأ: وهو الوقت اللازم لحل مُدخل مسألة حيث أن هذا المُدخل يستلزم أكثر وقت من بين كل المدخلات المحتملة التي لها نفس الطول.
• تعقيد الحالة المتوسطة: وهو متوسط الوقت اللازم لحل كل المدخلات التي لها نفس الطول، وهذا التعقيد يمكن حسابه فقط بعد ان نفرض توزيع الاحتمال على المُدخلات.

حدود عليا وحدود دنيا على تعقيد المسائل

لكي نصنف الوقت الحسابي للمسائل (أي الوقت اللازم لحل مسألة بواسطة نموذج حاسوبي معين) يجب على الشخص أن يبرهن الحدود الدنيا والعليا لكمية الوقت الاقل التي تستلزمها أفضل خوارزمية لحل المسألة، وبشكل عام تعقيد الخوارزمية هو تعقيد الحالة الأسوأ الا إذا حُدد غير ذلك، ولكي نبرهن أن لمسألة حد أعلى (T(n وجب تبيين خوارزمية التي تستلزم وقت (T(n. ولكن لكي نبرهن حد ادنى المهمة أصعب بكثير إذ على المرء أن يبين ان كل خوارزمية ممكنة لحل المسألة لا يوجد أي منها وقتها اقل من (T(n.

وللتوضيح: عندما نقول «كل خوارزمية» نعني أنه لا يمكن أن يكون هناك خوارزمية التي تستلزم وقتا اقل من (T(n حتى في المستقبل.

والحدود الدنيا والعليا لمسألة يعبر عنها بواسطة رمز O كبير.

اقسام تعقيد

تعريف

قسم تعقيد هو مجموعة مسائل التي لها نفس التعقيد، وقد تعرف أقسام التعقيد حسب العوامل التالية:

• نوع المسألة الحاسوبية: وفي هذا الباب نوع المسألة الأكثر شيوعا هي مسألة التقرير ولكن هنالك أيضا أنواع أخرى مثل مسائل دالة، مسائل عد، مسائل استمثال أو مسائل وعد...
• نموذج الحاسوبية: ولعل الأكثر شيوعا هي آلة تيورنج القطعية ولكن هنالك استخدام لآلة تيورنج غير القطعية، دارات منطقية، آلة تيورنج كمومية...
• الموارد التي يتم حصرها والحدود: مثل وقت متعدد الحدود، مكان لغرتمي، عمق ثابت...

هنالك تصنيفات أكثر تعقيدا من هذه المذكورة هنا مثل: آلة تيورنج احتمالية، الآلات تيورنج تفاعلية، مسائل اتصال...

اقسام تعقيد مهمة

كثير من أقسام التعقيد يمكن تعريفها بواسطة تحديد الوقت أو المكان التي تستخدمها الخوارزمية، وفي هذا السياق يمكن تعريف بعض الأقسام كالتالي:

اقسام تعقيد	النموذج الحاسوبي	قيود الموارد
((DTIME(f(n	آلة تيورنج قطعية	وقت (f(n
P	آلة تيورنج قطعية	وقت (poly(n
EXPTIME	آلة تيورنج قطعية	وقت(2poly(n
((NTIME(f(n	آلة تيورنج غير قطعية	وقت (f(n
NP	آلة تيورنج غير قطعية	وقت (poly(n
NEXPTIME	آلة تيورنج غير قطعية	وقت (2poly(n
((DSPACE(f(n	آلة تيورنج قطعية	مكان (f(n
L	آلة تيورنج قطعية	مكان (O(log n
بيسبايس	آلة تيورنج قطعية	مكان (poly(n
EXPSPACE	آلة تيورنج قطعية	مكان (2poly(n
((NSPACE(f(n	آلة تيورنج غير قطعية	مكان (f(n
NL (تعقيد حسابي)	آلة تيورنج غير قطعية	مكان (O(log n
بيسبايس	آلة تيورنج غير قطعية	مكان (poly(n
NEXPSPACE	آلة تيورنج غير قطعية	مكان (2poly(n

لقد تبين أن$NSPACE(f(n))\subseteq DSPACE(f^2(n))$ وكذلك: $PSPACE=NPSPACE$ و $EXPSPACE=NEXPSPACE$ وهذا كله بواسطة مبرهنة سافيتش (Savitch theorem).

أقسام مهمة أخرى من ضمنها ZPP , BPP ,Co-RP,RP وهي تستخدم آلة تيورنج احتمالية في تعريفها، أما BQP و QMA ففيهما استخدم آلة تيورنج كمومية، أما NC و- AC وكذلك P/Poly تعرف بواسطة الدارات المنطقية، أما بالنسبة ل-P# فهو قسم مسائل عد واحد أهمها على الإطلاق، أقسام مثل: IP و-AM تستخدم نظام براهين تفاعلي، ALL هو قسم كل المسائل.

مسائل كاملة

المقالة الرئيسية: مسألة كثيرة حدود غير قطعية كاملة

فلتكن $L\in \text{NP}$ نقول أنَّ $L$ مسألة $\text{NP}$ كاملة إذا تحقق:

• لكل $L^{\prime }\in \text{NP}$ يتحقق: $L^{\prime }{\le }_{p}L$

نسمي $\text{NP-complete}$ قسم اللغات التي هي NP كاملة.

بشكل مشابه يمكن تعريف مسائل كاملة في كل قسم لغات مثل: $\text{P,PSPACE},...$ .

إن المسائل الكاملة تعتبر «مسائل صعبة» بمفهوم انه لو وُجد حل بوقت حدودي لإحداها هذا يعني أن كل المسائل في $\text{ NP}$يمكن حلها بوقت حدودي.

النظرية التالية تشرح هذا الأمر:

$\text{NP-complete}\cap \text{P}\ne \mathrm{\varnothing }$ إذا وفقط إذا $\text{NP}=\text{P}$ .

مبرهنة كوك وليفين

المقالة الرئيسية: مبرهنة كوك وليفين

الاكتفاء (مسماة بالإنجليزية SAT) مسألة NP كاملة، وقد كانت هذه أول لغة يُبرهن انها NP كاملة، واهميتها كانت بانها الشرارة التي أوقدت نظرية التعقيد الحسابي والسعي وراء النماذج الحسابية المختلفة.

بعد أن تم برهنة أن مسألة الاكتفاء هي NP كاملة تبين أن الآلاف المسائل هي أيضا كذلك.

ولعل أهم المسائل كاملة هي:

1. مسألة الاكتفاء (SAT)
2. مشكلة تلوين المخطط.
3. مشكلة المخطط الكامل ضمن مخطط.
4. مشكلة الرحالة التاجر.
5. مسار هاملتونياني.

مبرهنات الهرمية

هذه المبرهنات تعتبر نتائج أساسية بواسطتها يمكن فصل أقسام التعقيد، والحدس خلف هذه المبرهنات هو إذا كان لديك موارد أكثر باستطاعتك ان تفعل أكثر، ولهذه المبرهنات عدة نصوص إذ أنه لكل مورد ومقياس تعقيد يوجد نص خاص به، وندرج بعض هذه:

• إذا كانت (f(n يمكن حسابها بوقت ((O(f(n حيث أن (log(n)<f(n حينها: $\text{DTIME(f(n))}⊊\text{DTIME(f(n)log(f(n)))}$
• فلتكن (s(n و- (g(n دالتين يمكن حسابهما بواسطة ((O(s(n و- ((O(g(n مكان حينها وإذا: (o(g(n))=s(n , حينها: $\text{SPACE(s(n))}⊊\text{SPACE(g(n))}$

ونتيجة لهذه المبرهنات فأننا نحصل على: $\text{P}\ne \text{EXP}$ وكذلك: $\text{NP}\ne \text{NEXP}$ وكذلك: $\text{L}\ne \text{PSPACE}$، كما أن هذه الاثباتات بشكل ما تناقض أطروحة ادموندز- كوبهام إذ انه هذا يعني أن هنالك مسائل لا يمكن حلها بوقت اقل من ${\text{n}}^{1000}$ وبشكل واضح هذا الوقت يُعتبر غير واقعي وغير قابل للوصول حتى بالنسبة ل- n=2 !

الاختصار

الاختصار (reduction) هو: وسيلة لنقل مسألة إلى مسألة أخرى، بحيث انه يمكن الاستعانة بحل المسألة الثانية لحل المسألة الأولى.

وقد شاع استخدام هذه الاختصارات في الحياة اليومية، مثال واضح على هذا هو: لنفرض اننا نريد ان نجد شارع في مدينة معينة لعل هذا يكون أسهل بوجود خريطة، إذا استخدمنا الخريطة نكون بهذا قد اختصرنا مسألة ايجاد الشارع في المدينة لإيجاد الشارع في الخريطة.

وبالعادة في الاختصارات عندنا مسألتين A و- B إذا فرضنا أن B يمكن اختصارها ل-A حينها حل المسألة A يمكن الاستعانة به لحل المسألة B، ولننظر إلى المسائل التالية:

1. السفر من إسطنبول إلى مكة.
2. شراء تذكرة طيران من إسطنبول إلى مكة.
3. جمع النقود لشراء التذكرة من إسطنبول إلى مكة.
4. إيجاد عمل لتحصيل النقود.

يمكن رؤية ان كل واحدة من المسائل يمكن اختصارها للأخرى بالشكل التالي: إذا حللنا مسألة ايجاد عمل حينها يمكن جمع النقود لشراء التذكرة من إسطنبول إلى مكة في الوقت الذي جمعنا فيه مالا كافيا لشراء التذكرة يمكن حينها شراء التذكرة وأخيرا السفر إلى مكة من إسطنبول.

كما ان الاختصارات تظهر كذلك في المسائل الرياضية مثل: قياس مساحة الدائرة يمكن اختصاره لإيجاد طول نصف القُطُر، كما انه يمكن اختصار حل هيئة معادلات خطية لعكس مصفوفة. يظهر الاختصار في كثير من المجالات في الرياضيات وذلك لانه بواسطة الاختصارات يمكن تصنيف مسائل الرياضيات إذ انه إذا يمكن اختصار مسألة A للمسألة B حينها المسألة A لا يمكن ان تكون أصعب من المسألة B، وهذه النظرة اخذها علوم الحاسوب لتصنيف الخوارزميات وقد تمكن علماء الحاسوب بناء نظرية التعقيد الحسابي بواسطتها.

يوجد عدة أنواع من الاختصارات ومنها:

1. اختصارات تورنغ: نقول ان اللغة $A\subseteq \{0,1{\}}^{*}$ يمكن اختصارها للغة $B\subseteq \{0,1{\}}^{*}$ إذا لكل $x\in A$ عدد خطوات* الحساب هو حدودي بالنسبة لطول المدخل أي $Poly(|x|)$ . * نقصد هنا بالخطوة الحسابية هو إما ان تكون خطوة حسابية بالمفهوم العادي أو تكون الخطوة هي الدخول لدالة تحل المسألة B.
2. اختصارات كارب أو قابلية اختصار بواسطة تطبيق حدودي: نقول أن لغة $A\subseteq \{0,1{\}}^{*}$ يمكن اختصارها بوقت حدودي للغة $B\subseteq \{0,1{\}}^{*}$ ويُرمز اليه ب- $A{\le }_{p}B$ إذا يوجد دالة يمكن حسابها بوقت حدودي $f:\{0,1{\}}^{*}\to \{0,1{\}}^{*}$ بحيث انه لكل $x\in \{0,1{\}}^{*}$ , $x\in A$ وفقط إذا $f(x)\in B$
3. اختصارات ليفين: فليكن f و- g دالتين يمكن حسابهما بوقت حدودي، حينها يمكن تسميتهما اختصار ليفين من اللغة R للغة 'R إذا كانت f اختصار كارب من $S_R=\{x:\mathrm{\exists }y,(x,y)\in R\}$ للغة ${S_R}^{\prime }=\{x:\mathrm{\exists }y,(x,y)\in R^{\prime }\}$ ولكل $x\in S_R$ وكذلك $y^{\prime }\in R^{\prime }(f(x))$ حينها $(x,g(x,y^{\prime }))\in R$ في حين أن $R^{\prime }(x^{\prime })=\{y^{\prime }:(x^{\prime },y^{\prime })\in R^{\prime }\}$ .
4. اختصارات سعة مواردها لُغَرِتمية: نبدأ أولا بتعريف نوع خاص من الدوال والتي هي يمكن حسابها بسعة موارد لغرتمية:
   فلتكن $f:\{0,1{\}}^{*}\to \{0,1{\}}^{*}$ دالة محدودة حدوديا بمعنى انه يوجد ثابت $c>0$ بحيث أن $f(x)\le |x{|}^c$ . ونقول أن f يمكن حسابها بسعة موارد لغرتمية إذا يمكن حساب اللغتين $L_f=\{⟨x,i⟩|f(x{)}_i=1\}$ وكذلك $L{\text{'}}_f=\{⟨x,i⟩|i\le |f(x)|\}$ يمكن حسابها بسعة موارد لغرتمية.
   والان نعرف اختصارات سعة مواردها لغرتمية بالشكل التالي: نقول أن لغة $A\subseteq \{0,1{\}}^{*}$ يمكن اختصارها بسعة موارد حدودية للغة $B\subseteq \{0,1{\}}^{*}$ ويُرمز اليه ب- $A{\le }_{l}B$ إذا يوجد دالة يمكن حسابها بسعة موارد لغرتمية $f:\{0,1{\}}^{*}\to \{0,1{\}}^{*}$ بحيث انه لكل $x\in \{0,1{\}}^{*}$ , $x\in A$ وفقط إذا $f(x)\in B$

مسائل غير محلولة

ظهرت مسائل في نظرية التعقيد ولعلها من أهم المسائل في الألفية، حيث ان تطور العلوم بشكل عام سيكون اسرع إذا حلت.

أهم هذه المسائل هي :

مسألة NP-P

من السهل ملاحظة أن المسائل الحتمية الحدودية (P) هي ضمن المسائل غير حتمية حدودية (NP)، لكن المسألة المقابلة والتي تسأل هل مجموعة المسائل غير حتمية مجموعة جزئية لمجموعة المسائل الحتمية؟ ولم يتمكن من الجواب عنها علماء المعلومات منذ سنة 1971 إلى الآن، هو هل هناك تساو أو اختلاف بين المجموعتين؟، وقد عُرض عام 2000 مكافئة قدرها مليون دولار لمن يحل المسألة وذلك بواسطة معهد كلاي.

تلقي هذه المسألة بظلها على كل مجالات العلوم الحديثة، ولحل هذه المسألة أهمية بالغة على تطور مجال علم التشفير، حيث انه لو NP=P حينها علم التشفير الحديث لن يكون له أي أهمية من الناحية النظرية، ولكن لو تحقق هذا فان مجال تصميم الشرائح الإلكترونية، تحليل الصور الرقمية، الذكاء الصناعي، وغيرها من المجالات ستتطور.

مسائل التي لا تتبع P ولا تتبع NP كاملة

لقد بيَّن لاندر انه في حال انه $\text{P}\ne \text{NP}$ حينها يوجد مسائل التي لا تتبع P ولا تتبع NP كاملة، للان لم يبرهن أحد على وجود مثل هذه المسائل، ولكن هنالك حدسيات عن بعض المسائل التي محتمل جدا ان تكون كذلك منها: تحليل لعوامل، تطابق المخططات (graph isomorphism), ...

التاريخ

من بين الأمثلة الأولى لتحليل تعقد الخوارزميات، عمل غابرييل لامي حول خوارزمية أقليدس. قام بهذا العمل في عام 1844.

انظر أيضا

• مسألة NP كاملة
• مسألة P-NP