نظام الإحداثيات الاستوائية

من أرابيكا، الموسوعة الحرة
اذهب إلى التنقل اذهب إلى البحث


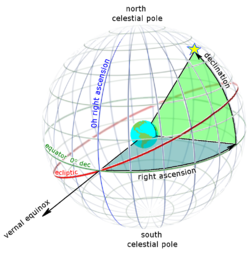
نظام الإحداثيات الاستوائية هو نظام إحداثيات سماوي يُستخدم على نطاق واسع لتحديد مواقع الأجرام السماوية. يمكن تضمينه في نظامي الإحداثيات الكروي أو الديكارتي، المحددان من نقطة أصل في مركز الأرض، وهو مستوى أساسي ينتج من إسقاط خط الاستواء على القبة السماوية (لتشكيل خط الاستواء السماوي)، واتجاه أساسي نحو نقطة الاعتدال الربيعي، ويتبع قاعدة اليد اليمنى.[1][2]

تعني نقطة الأصل في مركز الأرض أن الإحداثيات تتبع نموذج مركزية الأرض، أي مثلما تظهر من مركز الأرض كما لو كانت شفافة.[3] يعني المستوى والاتجاه الأساسيان أن نظام الإحداثيات، على الرغم من محاذاته لخط الاستواء والقطب الأرضي، لا يدور مع الأرض، ولكنه يبقى ثابتًا بالنسبة لنجوم الخلفية. تعني قاعدة اليد اليمنى أن الإحداثيات تزداد شمالًا وشرقًا حول المستوى الأساسي.

الاتجاه الأساسي

يُعتبر هذا الوصف لاتجاه الإطار المرجعي مبسطًا إلى حد ما؛ فالاتجاه ليس ثابتًا تمامًا. تسبب الحركة البطيئة لمحور الأرض، المعروفة باسم المبادرة المحورية، دوران نظام الإحداثيات ببطئ وباستمرار غربًا حول قطبي مسار الشمس، ليكمل دورةً واحدةً كل 26000 سنة تقريبًا. تتراكب على ذلك الحركة الأصغر لمسير الشمس نفسه، والتذبذب الصغير لمحور الأرض ، المعروف باسم التمايل.[4]

من أجل تحديد الاتجاه الأساسي الدقيق، تتطلب هذه الحركات تحديد الاعتدال الشمسي لتاريخ معين، المعروف باسم الحقبة، عند تحديد المواقع. الاعتدالات الأكثر استخدامًا هي:

  1. الإعتدال المتوسط للحقبة القياسية (عادةً «جاي 2000.0» ولكن قد يتضمن «بي 1950.0» و«بي 1900.0» إلخ.) هو اتجاه قياسي ثابت، يسمح بمقارنة المناطق، المعتمدة على تواريخ مختلفة، مباشرةً.
  2. الإعتدال المتوسط للتاريخ هو تقاطع مسار الشمس للـ «التاريخ» (أي مسار الشمس في موضعه في «التاريخ») مع خط الاستواء المتوسط (أي خط الاستواء الدوار نتيجة مبادرة موضعه في «التاريخ»، ولكن بدون وجود تذبذبات صغيرة ودورية أثناء حركة تمايل). يشيع استخدامه في حساب المدارات الكوكبية.
  3. الاعتدال الحقيقي للتاريخ هو تقاطع مسار الشمس لـ «التاريخ» مع خط الاستواء الحقيقي (أي خط الاستواء المتوسط بالإضافة إلى حركة التمايل). هذا هو التقاطع الفعلي بين المستويين في أي لحظة معينة، مع أخذ جميع الحركات بعين الاعتبار.

بالتالي، يُحدد الموقع في نظام الإحداثيات الاستوائية عادةً على أنه الاعتدال الحقيقي وخط استواء التاريخ والاعتدال المتوسط وخط الاستواء جاي 2000.0، أو ما يشابه ذلك. لاحظ أنه لا يوجد «مسار متوسط للشمس»، لأن مسار الشمس لا يخضع لتذبذبات دورية صغيرة.[5]

الإحداثيات الكروية

كما يُرى من فوق القطب الشمالي للأرض ،   الزاوية الساعية المحلية لنجم   (LHA) مراقب بالقرب من نيويورك. المفاهيم الممثلة في الصورة: المطلع المستقيم لنجم   والزاوية الساعية غرينتش   (GHA)، و متوسط الزمن الفلكي المحلي   (LMST) و متوسط الزمن الفلكي لغرينتش   (GMST). يحدد الرمز ʏ اتجاه نقطة الاعتدال الربيعي.

استخدامها في علم الفلك

غالبًا ما يُعبر عن الإحداثيات الكروية لنجم ما باستخدام زوجٍ من الإحداثيات، المطلع المستقيم والميل، بدون إحداثيات للمسافة. لا يختلف اتجاه الأجسام البعيدة من راصد إلى آخر، ومن المناسب تحديد هذا الاتجاه بنفس الإحداثيات للجميع. في المقابل، ففي نظام الإحداثيات الأفقي، يختلف موضع النجم من راصد إلى آخر اعتمادًا على موقعه على سطح الأرض، وهذا يتغير باستمرار مع دوران الأرض.تستخدم التلسكوبات، المجهزة بمحاور استوائية ودوائر ضبط، نظام الإحداثيات الاستوائية للرصد الأجرام في الفضاء. تسمح دوائر الضبط، المقترنة بخارطة للنجوم أو تقويم فلكي، بتوجيه التلسكوب بسهولة إلى الأجرام المعروفة في القبة السماوية.

خط الزوال

المقالة الرئيسية: خط الزوال

خط الزوال[6][7] أو خط الهاجرة[7] أو دائرة نصف النهار[7] هو دائرة عظمى وهمية في القبة السماوية، يمر من النقطة الشمالية في الأفق، عبر القطب السماوي إلى سمت الرأس، عبر النقطة الجنوبية للأفق، وعبر النظير عموديًا على خط الأفق.

المدارات اليومية

المدارات اليومية[8] أو دوائر الأزمان[9] (بالإنجليزية: Celestial parallels أو Parallels of declination)‏، هي دوائر وهمية موازية لخط الاستواء السماوي، وهي تحدد ميل نجم ما.

الدائرة الساعية

المقالة الرئيسية: دائرة ساعية

الدائرة الساعية[10] أو دائرة الميل[11] لأي جرم سماوي هي الدائرة العظمى التي تصل بين الجرم وبين الأقطاب السماوية ودائما ما تكون عمودية على خط الاستواء السماوي، كما أنها تمر بنجم ما وتحدد مطلعها المستقيم.

الميل

المقالة الرئيسية: ميل (علم الفلك)

يقيس الميل (يشار إليه بالحرف اليوناني الصغير دلتا δ) المسافة الزاوية لجسم عمودي على خط الاستواء السماوي، موجب في الشمال، وسالب في الجنوب. على سبيل المثال، يبلغ ميل القطب الشمالي السماوي +90 درجة. أصل الميل هو خط الاستواء السماوي، وهو إسقاط خط الاستواء الأرضي على الكرة السماوية. الانحراف مماثل لخط العرض الجغرافي. [12] [13] [14]

المطلع المستقيم

المقالة الرئيسية: مطلع مستقيم

يقيس المطلع المستقيم (يشار إليه بالحرف اليوناني الصغير ألفا α) المسافة الزاوية لجسم ما باتجاه الشرق على طول خط الاستواء السماوي من نقطة الاعتدال الربيعي إلى دائرة الساعة التي تمر عبر الجسم. نقطة الاعتدال الربيعي هي إحدى النقطتين اللتين يتقاطع فيهما مسار الشمس مع خط الاستواء السماوي. عادةً ما يُقاس المطلع المستقيم بالساعات الفلكية والدقائق والثواني بدلاً من الدرجات، نتيجة طريقة قياس المطلع المستقيم عن طريق تسجيل وقت مرور الأجسام عبر خط الزوال أثناء دوران الأرض. هناك360°/24h = 15 درجة في ساعة واحدة من المطلع المستقيم، و 24 ساعة من المطلع المستقيم حول خط الاستواء السماوي بأكمله. [12] [15] [16]

الزاوية الساعية

المقالة الرئيسية: زاوية ساعية

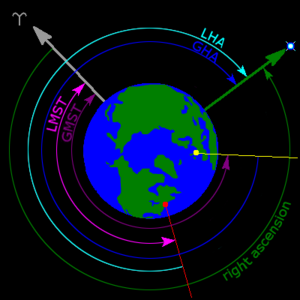
بدلاً من المطلع المستقيم، تقيس الزاوية الساعية المسافة الزاوية لجسم ما باتجاه الغرب على طول خط الاستواء السماوي من خط الزوال الخاص بالراصد إلى الدائرة الساعية التي تمر عبر الجسم. على عكس المطلع المستقيم، تتزايد الزاوية الساعية دائمًا مع دوران الأرض. يمكن اعتبار الزاوية الساعية وسيلة لقياس الوقت عند التكبد العلوي، اللحظة التي يعبر فيها الجسم خط الزوال.

يقال إن النجم الذي يتكبد على خط الزوال الخاص بالراصد له زاوية ساعية صفرية (0 ساعة). ساعة فلكية واحدة (حوالي 0.9973 ساعة شمسية) بعد ذلك، سيحمل دوران الأرض النجم إلى غرب خط الزوال، وستكون زاوية قدرها ساعة واحدة. عند حساب ظاهرة سمتية ارتفاعية، يمكن تحويل المطلع المستقيم إلى زاوية ساعية كخطوة وسيطة. [17] [18] [19]

انظر أيضًا

مراجع

  1. ^ Nautical Almanac Office, U.S. Naval Observatory؛ H.M. Nautical Almanac Office؛ Royal Greenwich Observatory (1961). Explanatory Supplement to the Astronomical Ephemeris and the American Ephemeris and Nautical Almanac. H.M. Stationery Office, London (reprint 1974). ص. 24, 26. مؤرشف من الأصل في 2016-03-13.
  2. ^ Vallado، David A. (2001). Fundamentals of Astrodynamics and Applications. Microcosm Press, El Segundo, CA. ص. 157. ISBN:1-881883-12-4.
  3. ^ U.S. Naval Observatory Nautical Almanac Office؛ U.K. Hydrographic Office؛ H.M. Nautical Almanac Office (2008). The Astronomical Almanac for the Year 2010. U.S. Govt. Printing Office. ص. M2, "apparent place". ISBN:978-0-7077-4082-9.
  4. ^ Explanatory Supplement (1961), pp. 20, 28
  5. ^ Meeus، Jean (1991). Astronomical Algorithms. Willmann-Bell, Inc., Richmond, VA. ص. 137. ISBN:0-943396-35-2.{{استشهاد بكتاب}}: صيانة الاستشهاد: التاريخ والسنة (link)
  6. ^ Q112315598، ص. 718، QID:Q112315598
  7. ^ أ ب ت المنجد في اللغة والأعلام (ط. 48). الأشرفية، بيروت: دار المشرق ش.م.م. 2014. ص. 183. ISBN:2-7214-2280-4.
  8. ^ محمد علي التهانوي. "كشاف+اصطلاحات+الفنون"+"الدائرة+المشرق+والمغرب"&hl=fr&sa=X&ved=2ahUKEwiXqdXoxcL6AhXci_0HHdJbD-YQ6AF6BAgGEAM#v=onepage&q="كشاف%20اصطلاحات%20الفنون"%20"الدائرة%20المشرق%20والمغرب"&f=false كشاف اصطلاحات الفنون 1-4. دار الكتب العلمية. ج. 2. ص. 106. مؤرشف من الأصل في 2022-10-02. ومدارات العرض، وتسمى بالمدارات العرضية و بالمدارات الطولية أيضًا، هي الدوائر المرتسمة من حركات النقاط المفروضة على فلك البروج سوى القطبين فعلى هذا ينبغي أن يجوز تسمية منطقة البروج بالمدار الطولي، كما يسمى معدل النهار بالمدار اليومي. هذا والمشهور أن المدارات اليومية هي الدوائر الصغار الموازية للمعدل، والمدارات العرضية هي الدوائر الصغار الموازية لمنطقة البروج .
  9. ^ محمد علي التهانوي (1853). "كشاف+اصطلاحات+الفنون"+"الدائرة+المشرق+والمغرب"&hl=fr&sa=X&ved=2ahUKEwiXqdXoxcL6AhXci_0HHdJbD-YQ6AF6BAgGEAM#v=onepage&q="كشاف%20اصطلاحات%20الفنون"%20"الدائرة%20المشرق%20والمغرب"&f=false كشاف اصطلاحات الفنون 1-4 ج2. دار الكتب العلمية. ص. 101. مؤرشف من الأصل في 2022-10-02.
  10. ^ سائر بصمه (1 يناير 2017). "periastron"+حضيض"&hl=fr&sa=X&ved=2ahUKEwiLi9mdrcv6AhWS7rsIHcKwDDkQ6AF6BAgEEAM#v=onepage&q=culmination&f=false القاموس الفلكي الحديث. دار الكتب العلمية. ص. 220. ISBN:978-2-7451-3066-2. مؤرشف من الأصل في 2022-10-08.
  11. ^ محمد علي التهناوي (1853). "كشاف+اصطلاحات+الفنون"+"الدائرة+المشرق+والمغرب"&hl=fr&sa=X&ved=2ahUKEwiXqdXoxcL6AhXci_0HHdJbD-YQ6AF6BAgGEAM#v=onepage&q="كشاف%20اصطلاحات%20الفنون"%20"الدائرة%20المشرق%20والمغرب"&f=false كشاف اصطلاحات الفنون 1-4. دار الكتب العلمية. ج. 2. ص. 101. مؤرشف من الأصل في 2022-10-02. دائرة الميل: هي عظيمة تمر بقطبي المعدل وبجزء ما من منطقة البروج أو بكوكب من الكواكب.
  12. ^ أ ب Peter Duffett-Smith (1988). Practical Astronomy with Your Calculator, third edition. مطبعة جامعة كامبريدج. ص. 28–29. ISBN:0-521-35699-7. مؤرشف من الأصل في 2022-05-31.
  13. ^ Meir H. Degani (1976). Astronomy Made Simple. Doubleday & Company, Inc. ص. 216. ISBN:0-385-08854-X. مؤرشف من الأصل في 2022-05-31.
  14. ^ Astronomical Almanac 2010, p. M4
  15. ^ Moulton، Forest Ray (1918). An Introduction to Astronomy. ص. 127. مؤرشف من الأصل في 2022-06-16.
  16. ^ Astronomical Almanac 2010, p. M14
  17. ^ Peter Duffett-Smith (1988). Practical Astronomy with Your Calculator, third edition. Cambridge University Press. ص. 34–36. ISBN:0-521-35699-7. مؤرشف من الأصل في 2022-05-30.
  18. ^ Astronomical Almanac 2010, p. M8
  19. ^ Vallado (2001), p. 154
مجلوبة من «https://3rabica.org/index.php?title=نظام_الإحداثيات_الاستوائية&oldid=1749636»