|
تضامنًا مع حق الشعب الفلسطيني |
منحنى لورنز

في علم الاقتصاد، يمثل منحنى لورنز رسمًا بيانيًا لتوزيع الدخل أو الثروة. طوره ماكس أو لورنز في عام 1905 لتمثيل عدم المساواة في توزيع الثروة.
المنحنى عبارة عن رسم بياني يوضح نسبة الدخل الإجمالي أو الثروة المفترضة لنسبة معينة من الأشخاص، على الرغم من أن هذا لا ينطبق بشكل صارم إذا كان عدد الأشخاص محدودًا (انظر أدناه). غالبًا ما يستخدم منحنى لورنز لتمثيل توزيع الدخل، حيث يظهر للنسبة ذات الدخل الادنى من الأسر، النسبة المئوية من إجمالي الدخل الذي يحصلون عليه. ترسم النسبة المئوية للأسر على المحور السيني، النسبة المئوية للدخل على المحور الصادي. يمكن استخدامه أيضًا لإظهار توزيع الأصول. في مثل هذا الاستخدام، يعتبر العديد من الاقتصاديين المنحنى مقياسًا لعدم المساواة الاجتماعية.
يفيد مفهوم منحنى لورنز في وصف التفاوت بين حجم الأفراد في علم البيئة[1] وفي دراسات التنوع البيولوجي، حيث ترسم النسبة التراكمية للأنواع مقابل النسبة التراكمية للأفراد، كما أنه مفيد في نمذجة الأعمال: في تمويل المستهلك، على سبيل المثال، لقياس النسبة المئوية الفعلية من حالات التخلف عن سداد الديون التي تُعزى إلى النسبة من الأشخاص الذين يعانون من أسوأ درجات المخاطر.
شرحه
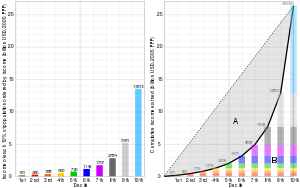
تمثل النقاط على منحنى لورنز عبارات مثل، «تحصل 20% من الأسر على 10% من إجمالي الدخل».
سيكون توزيع الدخل المتساوي تمامًا هو التوزيع الذي يحصل فيه كل الأشخاص على الدخل نفسه. في هذه الحالة، سيحصل نسبة معينة من المجتمع على نفس النسبة من الدخل. يمكن وصف ذلك بالخط المستقيم س = ص، ويسمى خط المساواة التامة.
على النقيض من ذلك، فإن التوزيع غير المتكافئ تمامًا هو التوزيع الذي يكون فيه لدى شخص واحد كل الدخل ولا يملك أي شخص آخر أي دخل. في هذه الحالة، سيكون المنحنى عند ص = 0% لجميع قيم س التي تكون أقل من 100%، و ص = 100% عندما تساوي س 100%. يسمى هذا المنحنى خط التفاوت التام.
معامل جيني هو نسبة المساحة بين خط المساواة التامة ومنحنى لورنز المرصود للمنطقة بين خط المساواة التامة وخط التفاوت التام. كلما زاد المعامل، كان التوزيع أقل تفاوتًا. في الرسم البياني على اليمين، يُعطى المعامل بواسطة النسبة A / (A + B)، حيث A و B مساحة المناطق كما هو موضح في الرسم التخطيطي.
خصائص منحنى لورنز
- يبدأ منحنى لورنز دائمًا عند (0،0) وينتهي عند (1،1).
- لم يُحدد منحنى لورنز في الحالات التي يكزن فيها متوسط التوزيع الاحتمالي صفرًا أو لانهائي.
- يمكن تلخيص المعلومات الموجودة في منحنى لورينز بواسطة معامل جيني ومعامل لورنز لعدم التماثل.[1]
- لا يمكن أن يرتفع منحنى لورينز فوق خط المساواة التامة.
- إذا كان المتغير الذي يقاس لا يمكن أن يأخذ قيمًا سالبة، فإن منحنى لورينز يبقى بحالة ازدياد ولا يمكن أن ينزل دون خط التفاوت التام.
مراجع
- ^ أ ب Damgaard، Christian؛ Jacob Weiner (2000). "Describing inequality in plant size or fecundity". Ecology. ج. 81 ع. 4: 1139–1142. DOI:10.1890/0012-9658(2000)081[1139:DIIPSO]2.0.CO;2.
| في كومنز صور وملفات عن: منحنى لورنز |