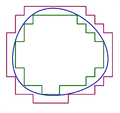
Made by myself with Matlab.
function main()
% the function whose zero level set and inner and outer approximations will be drawn
f = inline('60-real(z).^2-1.2*imag(z).^2-0.006*(real(z)-6).^4-0.01*(imag(z)-5).^4', 'z');
M=10; i=sqrt(-1); lw=2.5;
figure(1); clf; hold on; axis equal; axis off;
if 1==0
for p=-M:M
for q=-M:M
z=p+i*q;
if f(z)>0
plot(real(z), imag(z), 'r.')
else
plot(real(z), imag(z), 'b.')
end
end
end
end
% draw the zero level set of f
h=0.1;
XX = -M:h:M; YY = -M:h:M;
[X, Y] = meshgrid (XX, YY); Z = f(X+i*Y);
[C, H] = contour(X, Y, Z, [0, 0]);
set(H, 'linewidth', lw, 'EdgeColor', [0;0;156]/256);
% plot the outer polygonal curve
Start=5+6*i; Dir=-i; Sign=-1;
plot_poly (Start, Dir, Sign, f, lw, [139;10;80]/256);
% plot the inner polygonal curve
Sign=1; Start=4+5*i;
plot_poly (Start, Dir, Sign, f, lw, [0;100;0]/256);
% a dummy plot to avoid a matlab bug causing some lines to appear too thin
plot(8.5, 7.5, '*', 'color', 0.99*[1, 1, 1]);
plot(-4.5, -5, '*', 'color', 0.99*[1, 1, 1]);
saveas(gcf, 'jordan_illustration.eps', 'psc2');
function plot_poly (Start, Dir, Sign, f, lw, color)
Current_point = Start;
Current_dir = Dir;
Ball_rad = 0.03;
for k=1:100
Next_dir=-Current_dir;
% from the current point, search to the left, down, and right and see where to go next
for l=1:3
Next_dir = Next_dir*(Sign*i);
if Sign*f(Current_point+Next_dir)>=0 & Sign*f(Current_point+(Sign*i)*Next_dir) < 0
break;
end
end
Next_point = Current_point+Next_dir;
plot([real(Current_point), real(Next_point)], [imag(Current_point), imag(Next_point)], 'linewidth', lw, 'color', color);
round_ball(Current_point, Ball_rad, color'); % just for beauty, to round off some rough corners
Current_dir=Next_dir;
Current_point = Next_point;
end
function round_ball(z, r, color)
x=real(z); y=imag(z);
Theta = 0:0.1:2*pi;
X = r*cos(Theta)+x;
Y = r*sin(Theta)+y;
Handle = fill(X, Y, color);
set(Handle, 'EdgeColor', color);