|
تضامنًا مع حق الشعب الفلسطيني |
معامل لورنتز
معامل لورنتز في الفيزياء (بالإنجليزية: Lorenz Factor) كمية لا بعدية يستعملها الفيزيائيون في حساباتهم في النظرية النسبية الخاصة وتحديدا في حسابات تقلص الأطوال وتباطؤ الزمن.[1] ينسب هذا المعامل إلى العالم الهولندي هندريك أنتون لورنتس الذي صاغ ما يعرف بتحويلات لورنتز. ويعرف معامل لورنتز على أنه دالة في متغير وحيد وهو السرعة النسبية بين الراصد وجسم متحرك.
الصيغة الرياضية
رمز معامل لورنتز هو (جاما) ويساوي:
أو
حيث:
- مقسوم السرعة النسبية على سرعة الضوء،
- v السرعة النسبية
- c هي سرعة الضوء.
تقلص الأطوال
حيث
- L هو طول الجسم في حالة السكون.
- L' هو الطول الظاهر للراصد.
- هي السرعة النسبية بين الراصد والجسم المتحرك.
- هي سرعة الضوء،
ما معنى تقلص الطول؟
تنص النظرية النسبية على أن الأطوال تقصر «في اتجاه الحركة» وذلك عندما يقوم مشاهد خارج النظام بقياسها. وعلى سبيل المثال إذا افترضنا قطارا يسير بسرعة v مقاربة من سرعة الضوء c وبه راكب يقوم بقياسه ونفترض أن الطول الذي يحصل عليه داخل القطار L . ونفترض مشاهد واقف على رصيف المحطة يقوم هو أيضا بقياس القطار الذي يمرق أمامه بالسرعة v فهو يحصل على الطول L' . العلاقة بين الطولين يحددها معامل لورينتز الذي يعتمد على مربع النسبة بين سرعة القطار وسرعة الضوء طبقا للعلاقة أعلاه.
أي أن المشاهد الواقف على المحطة يقيس القطار المارق من أمامه بالطول L' بينما يقيسه راكب القطار (ويتحرك بنفس سرعة القطار) بالطول L ، وهذا ما تعنيه «النسبية»، أي نسبية قياس طول القطار بالنسبة لمشاهدين أحدهما يتحرك مع القطار ويقيسه والآخر يشاهده من المحطة، تختلف النتيجتان.
وكما تحدث نسبية قياس الأطوال وعلى الأخص عندما تقترب سرعة النظام المتحرك بسرعة مقاربة من سرعة الضوء فتصبح ملحوظة كذلك يكون قياس الزمن نسبي بالنسبة لشخص يتحرك مع الصاروخ وآخر واقف على منصة الإقلاع (انظر أسفله).
تباطؤ الزمن
- حيث
- فرق الزمن النسبي.
- فرق الزمن عند السكون.
ما معنى الإبطاء الزمني؟
بينت النظرية النسبية الخاصة أن الإبطاء الزمني يتبع معامل لورينتز. ولنفرض أن أحمد قد ركب صاروخ يسير بسرعة v (بالنسبة للأرض) ومع ساعة، وترك أخاه على الأرض ومعه ساعة من نفس الماركة. فعندما يقوم أحمد بقياس الزمن على ساعته ويمر عليه فترة ويقوم أخاه هاشم بقياس نفس الفترة فيحصل على الفترة الزمنية ، نجد أن الفترتين مختلفتين، ويتزايد اختلافهما بتزايد اقتراب سرعة الصاروخ من سرعة الضوء (في حياتنا اليومية لا نلاحظ تلك الفروق حيث أن سرعة تحركاتنا بطيئة جدا بمقارنتها بسرعة الضوء التي تبلغ 300.000 كيلومتر في الثانية). والنسبة بين سريان الزمن على الصاروخ ومسيرته على الأرض تعتمد على معامل لورينتز كما تبين المعادلة أعلاه التي تعتمد على مربع النسبة v/c .
بحسب مربع النسبة v/c نجد أن ساعة أحمد تبين مرور 50 دقيقة عنده في الوقت الذي تسجل فيه ساعة أخيه على الأرض مرور، مثلا 60 دقيقة.
فكلما اقتربت v من c كلما اقترب الكسر v/c من 1، وكلما اقترب الجزء من الصفر. بالتالي تزداد القيمة . وقد تحققنا من ذلك خلال تجارب كثيرة على طائرات وأقمار صناعية على تلك الإختلا فات التي يمكن حسابها بواسطة معامل لورينتز .
أي الأخين أكبر؟
نفترض أن أحمد عمره 31 سنة وعمر أخيه هشام 30 سنة. ونفترض أن أحمد ركب مركبة فضائية وقام بسفرية استغرقت وفق ساعته على الصاروخ سنتين فأصبح سنه 33 سنة، في نفس الوقت قد يمر على هشام على الأرض 5 سنوات فيصبح سنه 35 سنة. فعلا يمكن أن يحدث ذلك وأكثر عندما يتحرك أحمد بسرعة مقاربة من سرعة الضوء ويظل هشام على الأرض.
- اعترض بعض العلماء على تلك النتيجة وقت صياغة أينشتاين للنظرية النسبية وقالوا أنه بالنسبة إلى راصد خارج الأرض، على المريخ مثلا يشاهد المركبة الفضائية تخرج من الأرض وتؤدي رحلتها ثم تعود إلى الأرض. فرد عليهم أينشتاين أن ظروف المركبة الفضائية وظروف الأرض تختلفان، إذ أن مركبة الفضاء (وأحمد عليها) هما الذان عانا عمليات التعجيل والكبح.
الولد وأبوه
نفترض أن الأب رائد فضاء بدأ رحلته بالصاروخ وعمره 40 سنة وكان ابنه مولودا عمره سنة واحدة، ثم مر على الوالد في الصاروخ مدة أربعة سنوات حتى عودته إلى الأرض. قد تعادل الأربعة سنوات على الصاروخ السريع أربعين سنة على الأرض (تصل قيمة = 10 عندما تكون سرعة الأب 993و0 من سرعة الضوء). فيصبح سن الأب عند عودته 44 سنة ويجد ابنه في سن 41 سنة. بل إذا زادت سرعة الصاروخ أكثر من ذلك فقد يعود الأب إلى الأرض في سن 44 سنة ويجد أبنه في سن 50 سنة !! والمهم هو استمرار طيران الأب بسرعة مقاربة من سرعة الضوء.
تزايد الكتلة
تتزايد كتلة الأجسام كلما اقتربت سرعتها من سرعة الضوء البالغة 300.000 كيلومتر في الثانية. وفعلا عينت تلك الزيادة في المختبرات حيث تعجل جسيمات مثل البروتون في معجل مع قياس كتلتها، وقياس زيادة كتلتها بزيادة سرعاتها. هذه هي إحدى نتائج النظرية النسبية الخاصة لأينشتاين التي صاغها عام 1905 . والعلاقة الخاصة بتزايد الكتلة بزيادة سرعة الجسم تقول أن:
- حيث
- m' الكتلة النسبية أو كتلة الجسيم المتحرك،
- m كتلة السكون.
ينتج من تلك العلاقة أن جسما لا يمكن من الوجهة العملية أن تبلغ سرعته سرعة الضوء، إذ أن تسريع الجسم يحتاج إلى طاقة وكلما زادت كتلة الجسم احتاج لتسريعه طاقة أكبر، وزيادة سرعته تزيد من كتلته فبالتالي يحتاج إلى طاقة أكبر فأكبر لتسريعه أكثر حتى تصبح الطاقة اللآزمة لتسريعه لا نهائية، أي لا يمكن تحضيرها عمليا.
وصل مصادم الهدرونات الكبير إلى تسريع البروتونات إلى أن تصل كتلة البروتون نحو 200 بروتون، أي تعادل كتلة البروتون المسرّع نحو كتلة ذرة الرصاص.
يبين الجدول المنشور اسفله تحت عنوان «قيمته» أن معامل لورينتز يصل إلى نحو = 22 عندما تصل سرعة الجسم أو الجسيم 999و0 من سرعة الضوء.
قيمته
عند تكون السرعة النسبية بين الراصد والمتحرك صفر فإن معامل لورنتز يأخذ أدنى قيمة له وهي واحد.أما حين يتحرك الجسم بسرعة تناهز سرعة الضوء ُفإن معامل لورنتز يزداد بشكل كبير.وقد يؤول إلى مالانهاية إذا بلغت السرعة النسبية بين الراصد والمتحرك سرعة الضوء.
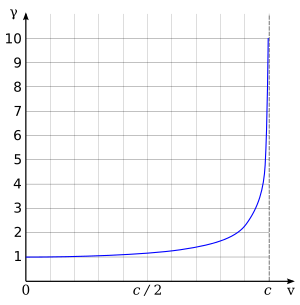
| السرعة | معامل لورنتز | المقلوب |
|---|---|---|
| 0.000 | 1.000 | 1.000 |
| 0.100 | 1.005 | 0.995 |
| 0.200 | 1.021 | 0.980 |
| 0.300 | 1.048 | 0.954 |
| 0.400 | 1.091 | 0.917 |
| 0.500 | 1.155 | 0.866 |
| 0.600 | 1.250 | 0.800 |
| 0.700 | 1.400 | 0.714 |
| 0.800 | 1.667 | 0.600 |
| 0.866 | 2.000 | 0.500 |
| 0.900 | 2.294 | 0.436 |
| 0.990 | 7.089 | 0.141 |
| 0.999 | 22.366 | 0.045 |
انظر أيضا
- النظرية النسبية الخاصة
- تقلص الأطوال
- تحويل لورينتز
- أشخاص: آرثر إيدينجتون | ألبرت آينشتاين | هيندريك لورينتز | هيرمان مينكوفسكي | بيرنارد ريمان | هنري بوانكارييه | اليكسندر ماكفارلين | هاري باتيمان | روبرت شانكلاند | بلو وييلر
- النسبية: نظرية النسبية.
وصلات خارجية
روابط عربية (بالعربية)
روابط إنجليزية (بالإنجليزية)
- شروح هوغ عن النسبية مقدمة جيدة عن النسبية للمستوى الجامعي.
- حاسبة النسبية لعمل حسابات هندسية في المسائل النسبية كما في جمع السرع. التطبيق يتطلب جافا وقد يستغرق عدة دقائق للتحميل إذا كان الاتصال بطيئا.
- السياق التاريخ للنسبية: اكتشاف النسبية الخاصة كان أمرا حتميا إذا ما أخذت الاكتشافات التي سبقته بعين الاعتبار.
- لا شيء سوى النسبية فهنالك عدة طرق لاشتقاق تحويلات لورينتز من دون استخدام فرضية أينشتاين عن ثبوت الضوء. الأسلوب المتبع في هذه الورقة يعيد صياغة أسلوب معروف وبسيط.
- تأملات في النسبية كتاب إلكتروني كامل عن النسبية مع قائمة مطولة بالمراجع.
- محاضرات عن النسبية الخاصة عبارة عن مقدمة تقليدية لموضع النسبية الخاصة يحتوي على أمثلة توضيحية بناء على رسومات ومخططات زمكانية من جامعة فيرجينيا التقنية.
- نظرية النسبية الخاصة بشكل مبسط أسلوب جديد لشرح المعنى النظري للنسبية الخاصة من وجهة نظر هندسية مبسطة.
- النسبية الخاصة جامعة ستانفورد، هيلين كوين، 2003*قالب:غوتبرغ, تأليف: ألبرت أينشتاين
- بعيني أينشتاين الجامعة الوطنية الأسترالية. تأثيرات بصرية نسبية مشروحة بواسطة الصور والأفلام.
- أساسيات كريغ إيغان
- ضوء أينشتاين مقدمة غير تقنية فائزة بجائزة.
- أفكار منيرة رسوم متحركة فكاهية عن النسبية الخاصة لعامة الناس، يانيك ماهي، 2005
- محاكي راب للنسبية الخاصة برنامج حاسوبي يوضح تأثير السفر بسرعة قريبة من سرعة الضوء
مراجع
- ^ "معلومات عن معامل لورنتز على موقع zthiztegia.elhuyar.eus". zthiztegia.elhuyar.eus. مؤرشف من الأصل في 2019-06-11.
| في كومنز صور وملفات عن: معامل لورنتز |