عمود تايلور

حركة السائل فوق وتحت جسم متحرك يضطر إلى الدوران ، وبالتالي يقتصر على أن يكون داخل عمود ممتد بواسطة الكائن في محور الدوران.

عمود تايلور هو ظاهرة ديناميكية الموائع التي تحدث نتيجة لتأثير كوريوليس. سميت على اسم جيفري إنجرام تايلور. تميل السوائل الدوارة التي يزعجها جسم صلب إلى تشكيل أعمدة موازية لمحور الدوران تسمى أعمدة تايلور.

جسم يتحرك بالتوازي مع محور الدوران في سائل دوار يواجه قوة سحب أكبر مما قد يتعرض له في سائل غير دوار. على سبيل المثال ، سترتفع كرة قوية الطفو (مثل كرة بينج بونج) إلى السطح أبطأ مما لو كانت في سائل غير دوار. هذا لأن السائل الموجود في مسار الكرة الذي يتم دفعه بعيدًا عن الطريق يميل إلى الدوران عائدًا إلى النقطة التي يتم تحريكها بعيدًا عنها ، بسبب تأثير كوريوليس. كلما كان معدل الدوران أسرع ، قل نصف قطر الدائرة بالقصور الذاتي التي يقطعها السائل.

يتم دفع وحدة من السوائل (ممثلة بالنقطة السوداء) إلى النقطة التي يتم تحويلها منها.

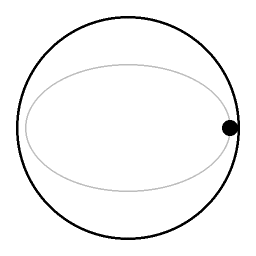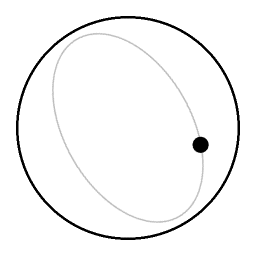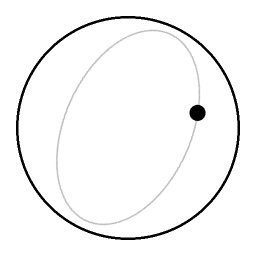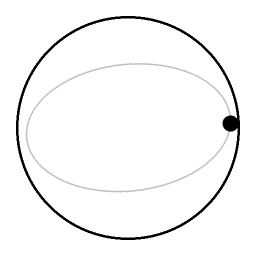
في سائل غير دوار ، الأجزاء السائلة فوق الكرة الصاعدة وتنغلق في تحتها ، مما يوفر مقاومة قليلة نسبيًا للكرة. في السائل الدوار ، تحتاج الكرة إلى دفع عمود كامل من السائل فوقه ، وتحتاج إلى سحب عمود كامل من السائل تحته من أجل الارتفاع إلى السطح.

وبالتالي فإن السائل الدوار يعرض درجة معينة من الصلابة.

التاريخ

وقد لوحظت أعمدة تايلور لأول مرة من قبل وليام طومسون ، اللورد كلفن، في عام 1868. تم عرض أعمدة تايلور في محاضرات توضيحية من قبل كلفن في عام 1881 وبواسطة جون بيري في عام 1890. يتم شرح الظاهرة عبر نظرية تايلور برودمان، وقد تم التحقيق فيها من قبل تايلور, غريس, ستيوارتسون, و ماكسوورثي- من بين أمور أخرى.

النظرية

تايلور العمود في السائل

تم دراسة أعمدة تايلور بدقة. ل إعادة<<1, إك<<1, رو<<1 ، معادلة السحب لأسطوانة نصف قطرها, a، تم العثور على العلاقة التالية.

$F=\frac{16}{3}\rho a^3\mathrm{\Omega }U$

لاستخلاص هذا ، حل مور وسافمان الخطية معادلة نافير-ستوكس جنبا إلى جنب في إحداثيات أسطوانية, حيث يتم اعتبار بعض المكونات الرأسية والشعاعية للمصطلح اللزج صغيرة بالنسبة لمصطلح كوريوليس:

$-2\mathrm{\Omega }v=-\frac{1}{\rho }\frac{\partial p}{\partial r}$

$2\mathrm{\Omega }u=\nu (\frac{{\partial }^{2}v}{\partial r^2}+\frac{1}{r}\frac{\partial v}{\partial r}-\frac{v^2}{r})$

$0=-\frac{1}{\rho }\frac{\partial p}{\partial z}+\nu (\frac{{\partial }^{2}w}{\partial r^2}+\frac{1}{r}\frac{\partial w}{\partial r})$

لحل هذه المعادلات ، نقوم بدمج شرط الحفاظ على الحجم أيضًا:

$\frac{1}{r}\frac{\partial (ur)}{\partial r}+\frac{\partial w}{\partial z}=0$

نستخدم علاقة توافق Ekman لهذه الهندسة لتقييد شكل السرعة على سطح القرص:

$w-U=\pm \frac{1}{2}\sqrt{\frac{\nu }{\mathrm{\Omega }}}\frac{1}{r}\frac{\partial (rv)}{\partial r}$

يمكن حل حقول السرعة الناتجة من حيث وظائف بسل.

$u=-\frac{\nu }{2\mathrm{\Omega }}\underset{0}{\overset{\mathrm{\infty }}{\int }}{k}^{2}A(k)J_1(kr)e^{-\nu k^{3}z/2\mathrm{\Omega }}dk$

$v=\underset{0}{\overset{\mathrm{\infty }}{\int }}A(k)J_1(kr)e^{-\nu k^{3}z/2\mathrm{\Omega }}dk$

$w=-\underset{0}{\overset{\mathrm{\infty }}{\int }}A(k)J_0(kr)e^{-\nu k^{3}z/2\mathrm{\Omega }}dk$

حيث ل إك< < 1 وظيفة أ (ك) تعطى من قبل,

$A(k)=\frac{2Ua}{\pi }(\cos ka-\frac{\sin ka}{ka})$

بدمج معادلة v ، يمكننا إيجاد الضغط وبالتالي قوة السحب المعطاة في المعادلة الأولى.

مزيد من القراءة

• Brenner، Michael P.؛ Stone، Howard A. (مايو 2000). "Modern Classical Physics Through the Work of G. I. Taylor". Physics Today. ج. 53 ع. 5: 30–35. Bibcode:2000PhT....53e..30B. DOI:10.1063/1.883100.

روابط خارجية

• أعمدة تايلور (مارثا باكلي, معهد ماساتشوستس للتكنولوجيا)
• ديناميات السوائل لاعب سجل: تجربة عمود تايلور (جامعة كاليفورنيا سبين مختبر)