|
تضامنًا مع حق الشعب الفلسطيني |
علم البيئة النظري
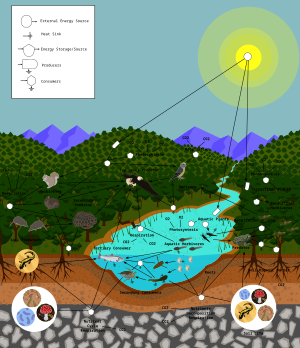
علم البيئة النظري هو المنهج العلمي المكرَّس لدراسة النظم البيئية باستخدام الأساليب النظرية مثل النماذج النظرية البسيطة والنماذج الرياضية والمحاكاة الحاسوبية والتحليل المتقدم للبيانات. تعمل النماذج الفعالة على تحسين فهم العالم الطبيعي من خلال الكشف عن كيفية استناد ديناميات مجموعات الأنواع إلى الظروف والعمليات البيولوجية الأساسية. أضف إلى ذلك أن هذا المجال يهدف إلى توحيد مجموعة متنوعة من الملاحظات التجريبية من خلال افتراض أن العمليات الآلية المشتركة تولّد ظواهر يمكن ملاحظتها عبر الأنواع والمحيطات البيئية. استنادًا إلى افتراضات واقعية بيولوجيًا، يستطيع علماء البيئة النظرية اكتشاف لمحات جديدة غير بديهية حول العمليات الطبيعية. غالبًا ما يتم التحقق من النتائج النظرية من خلال الدراسات التجريبية والرصدية، ما يكشف عن قوة الأساليب النظرية في التنبؤ وفهم العالم البيولوجي الصاخب والمتنوع.
علم البيئة النظري مجال واسع ويشمل الأسس في الرياضيات التطبيقية وعلوم الكمبيوتر والأحياء والفيزياء الإحصائية وعلم الوراثة والكيمياء والتطور وبيولوجيا الحفظ. يهدف علم البيئة النظري إلى توضيح مجموعة متنوعة من الظواهر في علوم الحياة مثل نمو المجتمعات ودينامياتها، والثروات السمكية والمنافسة ونظرية التطور وعلم الأوبئة وسلوك الحيوان وديناميات المجموعات والشبكات الغذائية والنظم البيئية والبيئة المكانية وآثار تغير المناخ.
استفاد علم البيئة النظري من ظهور قوة الحوسبة السريعة، ما سمح بتحليل وتصور المحاكاة الحاسوبية واسعة النطاق للظواهر البيئية. الأهم من ذلك هو أن هذه الأدوات الحديثة توفر تنبؤات كمية حول آثار التغير البيئي الناجم عن الأنشطة البشرية على مجموعة متنوعة من الظواهر البيئية، مثل: غزو الأنواع وتغير المناخ وتأثير الصيد البري والبحري على استقرار شبكة الأغذية ودورة الكربون العالمية.
تصنيف المقاربات
كما هو الحال في معظم العلوم الأخرى، تشكل النماذج الرياضية أساس النظرية البيئية الحديثة.
- النماذج الظواهرية: استخلاص الأشكال الوظيفية والتوزيعية من الأنماط الملحوظة في البيانات، أو يقرر الباحثون الوظائف والتوزيعات التي تكون مرنة بما يكفي لمطابقة الأنماط التي وجدوها هم أو وجدها آخرون (علماء البيئة الحقلية أو التجريبية) في الحقل أو من خلال التجارب.[3]
- النماذج الميكانيكية: صياغة العمليات الأساسية مباشرة، مع الوظائف والتوزيعات التي تستند إلى الاستدلال النظري حول العمليات البيئية موضع الاهتمام.[3]
يمكن للنماذج البيئية أن تكون حتمية أو تصادفية.[3]
- تتطور النماذج الحتمية دائمًا بنفس الطريقة من نقطة انطلاق معينة.[4] تمثل السلوك المتوسط والمتوقع للنظام، لكنها تفتقر إلى التغير العشوائي. العديد من نماذج ديناميات النظام حتمية.
- تسمح النماذج التصادفية بالنمذجة المباشرة للاضطرابات العشوائية التي تشكل أساس النظم البيئية في العالم الحقيقي. نماذج سلسلة ماركوف هي مؤشر تصادفي.
يمكن نمذجة الأنواع في زمن مستمر أو متقطع.[5]
- يُصمم الزمن المستمر باستخدام المعادلات التفاضلية.
- يُقسم الزمن المتقطع باستخدام معادلات الاختلاف. هذه العمليات البيئية النموذجية التي يمكن وصفها بأنها تحدث على مراحل زمنية متقطعة. غالبًا ما تُستخدم المصفوفة لاستقصاء تطور المجموعات عمرية البنية أو مرحلية البنية. تمثل مصفوفة ليزلي على سبيل المثال، التغير المتقطع للوقت لمجموعة عمرية البنية.[6][7][8]
غالبًا ما تستخدم النماذج لوصف عمليات التكاثر البيئي الحقيقية لأحد الأنواع أو لأنواع المتعددة. يمكن تشكيل هذه النماذج باستخدام عمليات المتفرعة العشوائية. من الأمثلة على ذلك نجد ديناميات المجموعات المتفاعلة (منافسة الافتراس والتكافل)، والتي، وفقًا للأنواع موضع الاهتمام، قد تشكّل على فترة زمنية مستمرة أو متقطعة. يمكن العثور على أمثلة أخرى لهذه النماذج في مجال الوبائيات الرياضية إذ تكون العلاقات الديناميكية التي ستجري صياغتها هي تفاعلات مُضيف - مُمرض.[5]
تُستخدم نظرية التشعب لتوضيح كيف يمكن أن تؤدي التغييرات الصغيرة في قيم المعايير إلى نتائج طويلة المدى مختلفة اختلافًا جذريًا، وهي حقيقة رياضية يمكن استخدامها لتفسير الاختلافات الإيكولوجية الحادة التي تحدث في أنظمة متشابهة نوعيًا إلى حد كبير.[9] الخرائط اللوجيستية هي خرائط كثيرة الحدود، ويُستشهد بها غالبًا كأمثلة نموذجية لكيفية ظهور السلوك الفوضوي من معادلات ديناميكية غير خطية بسيطة للغاية. روّج عالم البيئة النظري روبرت ماي لهذه الخرائط في ورقة بحثية عام 1976.[10]
عام 1930، نشر آر. آي. فيشر كتابه الكلاسيكي «النظرية الوراثية للانتقاء الطبيعي»، الذي قدم فكرة أن اللياقة المعتمدة على التردد تجلب جانبًا استراتيجيًا للتطور، إذ تكون مكافأة كائن معين، الناشئة عن تفاعل جميع الكائنات ذات الصلة، هي عدد الذريّات القابلة للحياة التي ينجبها هذا الكائن الحي.[11] عام 1961، طبق ريتشارد ليونتين نظرية الألعاب على البيولوجيا التطورية في كتابه «التطور ونظرية الألعاب»،[12] أتبعه بعد وقت قصير جون ماينارد سميث بمقال نشره عام 1972 بعنوان «نظرية الألعاب وتطور القتال» حدد فيه مفهوم إستراتيجية مستقرة تطوريًا.[13]
لأن النظم البيئية عادةً تكون غير خطية، فهي في كثير من الأحيان غير قابلة للحل بأسلوب تحليلي، ولكي نحصل على نتائج معقولة، يجب أن نستخدم التقنيات غير الخطية والعشوائية والحسابية. هناك فئة محددة من النماذج الحسابية تكسب شعبية شعبية متزايدة هي النماذج اقائمة على العوامل. يمكن أن تحاكي هذه النماذج الإجراءات والتفاعلات للكائنات المتعددة غير المتجانسة إذ تكون التقنيات التحليلية التقليدية غير كافية. يولّد علم البيئة النظري التطبيقي نتائج قابلة للاستخدام في العالم الواقعي.[14]
علم البيئة التطوري
اشتهر عالم الأحياء البريطاني ألفريد راسل والاس باقتراحه بشكل مستقل نظرية التطور بسبب الاصطفاء الطبيعي وهو ما دفع العالم تشارلز داروين إلى نشر نظريته الخاصة. في مقالته الشهيرة لعام 1858، اقترح والاس الانتقاء الطبيعي كنوع من آلية التغذية الراجعة التي تبقي الأنواع والأصناف متكيفة مع بيئتها.[15]
التاريخ
يعتمد علم البيئة النظري على العمل الرائد الذي قام به جي. إيفلين هتشينسون وطلابه. يعتبر الأخوان أودوم مؤسسي علم البيئة النظري الحديث.[16]
أضاف سيمبرلوف الدقة الإحصائية إلى علم البيئة التجريبي وكان شخصية رئيسية في مناظرة «سلوس» حول ما إذا كان من الأفضل حماية احتياطي كبير واحد أو عدة احتياطيات صغيرة.[17]
علماء البيئة النظرية وعلماء البيئة الرياضية
يمكن التمييز بشكل مبدئي بين علماء البيئة الرياضية وعلماء البيئة الذين يطبقون الرياضيات على المشكلات البيئية وعلماء الرياضيات الذين يطورون الرياضيات نفسها التي تنشأ من مشاكل بيئية.
انظر أيضًا
مراجع
- ^ May RM (2001) Stability and Complexity in Model Ecosystems Princeton University Press, reprint of 1973 edition with new foreword. (ردمك 978-0-691-08861-7). نسخة محفوظة 30 يوليو 2016 على موقع واي باك مشين.
- ^ Pimm SL (2002) Food Webs University of Chicago Press, reprint of 1982 edition with new foreword. (ردمك 978-0-226-66832-1). نسخة محفوظة 13 مارس 2020 على موقع واي باك مشين.
- ^ أ ب ت Bolker BM (2008) Ecological models and data in R Princeton University Press, pages 6–9. (ردمك 978-0-691-12522-0). نسخة محفوظة 13 مارس 2020 على موقع واي باك مشين.
- ^ Sugihara G، May R (1990). "Nonlinear forecasting as a way of distinguishing chaos from measurement error in time series" (PDF). Nature. ج. 344 ع. 6268: 734–41. Bibcode:1990Natur.344..734S. DOI:10.1038/344734a0. PMID:2330029. مؤرشف من الأصل (PDF) في 2011-08-14. اطلع عليه بتاريخ 2011-05-13.
- ^ أ ب Soetaert K and Herman PMJ (2009) A practical guide to ecological modelling Springer. (ردمك 978-1-4020-8623-6). نسخة محفوظة 13 مارس 2020 على موقع واي باك مشين.
- ^ Grant WE (1986) Systems analysis and simulation in wildlife and fisheries sciences. Wiley, University of Minnesota, page 223. (ردمك 978-0-471-89236-6).
- ^ Jopp F (2011) Modeling Complex Ecological Dynamics Springer, page 122. (ردمك 978-3-642-05028-2). نسخة محفوظة 13 مارس 2020 على موقع واي باك مشين.
- ^ Burk AR (2005) New trends in ecology research Nova Publishers, page 136. (ردمك 978-1-59454-379-1). نسخة محفوظة 13 مارس 2020 على موقع واي باك مشين.
- ^ Ma T and Wang S (2005) Bifurcation theory and applications World Scientific. (ردمك 978-981-256-287-6). نسخة محفوظة 13 مارس 2020 على موقع واي باك مشين.
- ^ May، Robert (1976). Theoretical Ecology: Principles and Applications. Blackwell Scientific Publishers. ISBN:978-0-632-00768-4.
- ^ Fisher، R. A. (1930). The genetical theory of natural selection. Oxford: The Clarendon press. مؤرشف من الأصل في 2019-03-28.
- ^ R C Lewontin (1961). "Evolution and the theory of games". Journal of Theoretical Biology. ج. 1 ع. 3: 382–403. DOI:10.1016/0022-5193(61)90038-8.
- ^ John Maynard Smith (1974). "Theory of games and evolution of animal conflicts" (PDF). Journal of Theoretical Biology. ج. 47 ع. 1: 209–21. DOI:10.1016/0022-5193(74)90110-6. PMID:4459582. مؤرشف من الأصل (PDF) في 2017-08-08.
- ^ Supriatna AK (1998) Optimal harvesting theory for predator–prey metapopulations University of Adelaide, Department of Applied Mathematics. نسخة محفوظة 13 مارس 2020 على موقع واي باك مشين.
- ^ Smith، Charles H. "Wallace's Unfinished Business". Complexity (publisher Wiley Periodicals, Inc.) Volume 10, No 2, 2004. مؤرشف من الأصل في 2009-01-29. اطلع عليه بتاريخ 2007-05-11.
- ^ Cuddington K and Beisner BE (2005) Ecological paradigms lost: routes of theory change Academic Press. (ردمك 978-0-12-088459-9). نسخة محفوظة 13 مارس 2020 على موقع واي باك مشين.
- ^ Soulé ME، Simberloff D (1986). "What do genetics and ecology tell us about the design of nature reserves?" (PDF). Biological Conservation. ج. 35 ع. 1: 19–40. DOI:10.1016/0006-3207(86)90025-X. مؤرشف من الأصل (PDF) في 2012-03-15.
| علم البيئة النظري في المشاريع الشقيقة: | |