|
تضامنًا مع حق الشعب الفلسطيني |
دائرتان توأم

في الهندسة، الدائرتان التوأمتان (بالإنجليزية: Twin circles) هما دائرتان خاصتان مرتبطتان بـ أربيلوس arbelos، الذي يتحدد شكله من خلال ثلاث نقاط على خط واحد A وB وC، وهي المنطقة المثلثية المنحنية بين الدوائر الثلاثة التي يكون أقطارها هي: AB وBC وAC. إذا جرى تقسيم أربيلوس إلى منطقتين صغيرتين بقطعة مستقيمة عبر النقطة الوسطى B، بخط متعامد مع الخط AC، فإن كل دائرة من الدائرتين التوأمتين تقع داخل إحدى هاتين المنطقتين، وتكون متماسة مع نصف الدائرة الخارجية ونصف الدائرة الداخلية والقطعة المستقيمة التي قسمت الـ أربيلوس (لاحظ الدائرتين في الشكل المجاور).
ظهرت هذه الدوائر لأول مرة في كتاب الليماس Book of Lemmas والذي ورد فيه في (الاقتراح الخامس) أن الدائرتين متطابقتين.[1] قام ثابت بن قرة بترجمة هذا الكتاب إلى اللغة العربية، ونسبه إلى العالِم اليوناني في الرياضيات أرخميدس. بناء على هذا الافتراض تُسمى الدوائر التوأم المتطابقة والموجودة في الـ أربيلوس بـ «دوائر أرخميدس». ومع ذلك، فقد شككت دراسة لاحقة في إسناد ذلك إلى أرخميدس.[2]
تكوينهما
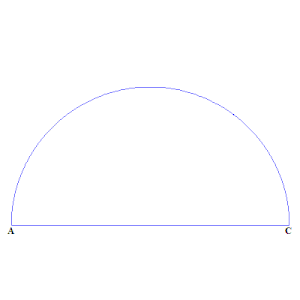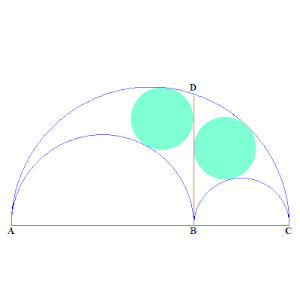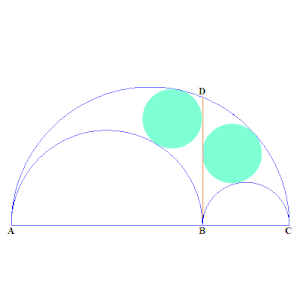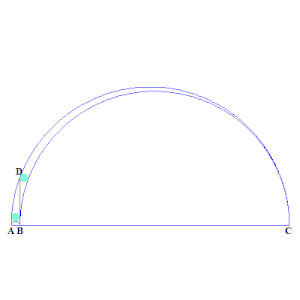
نفرض أن النقاط و، و هي أركان الـ أربيلوس الثلاثة، حيث بين و (طالع الرسم المتحرك). ونفرض هي النقطة التي يتقاطع فيها نصف الدائرة الأكبر مع الخط العمودي على المرسوم من النقطة . القطعة تقسم الـ أربيلوس إلى قسمين. الدائرتان التوأمتان هما دائرتان مرسومتان في هذين الجزأين، كل منهما تمس إحدى نصفي الدائرتين الأصغر، وتمس القطعة ، وتمس نصف الدائرة الأكبر.[3]
يجري تحديد كل دائرة من الدائرتين بشكل منفصل من خلال تماساتها الثلاثة. ويُعد هذا حالة خاصة لمسألة أبولونيوس.
عُثر على طرق بديلة لتكوين دائرتين متطابقتين مع الدائرتين التوأمتين.[4][5] وقد سميت هذه الدوائر أيضًا بدوائر أرخميدس. وهي تشمل دائرة Bankoff ودوائر Schoch ودوائر Woo.
الخصائص
لنفترض أن a وb هما أقطار نصفي الدائرتين الداخليتين، بحيث يكون قطر نصف الدائرة الخارجية هو a + b. يمكن حساب قطر كل دائرة من الدائرتين التوأمتين d من المعادلة:[6]
بدلاً من ذلك، إذا كان نصف الدائرة الخارجية قُطرها الوحدة (=1)، ونصفي الدائرتين الداخليتين لها أقطار و، فإن قطر كل دائرة من الدائرتين التوأمتين هو
أصغر دائرة تحيط بكلتا الدائرتين التوأمتين تكون مساحتها هي نفس مساحة الـ أربيلوس.
المراجع
- ^ Thomas Little Heath (1897), The Works of Archimedes. Cambridge University Press. Proposition 5 in the Book of Lemmas. Quote: "Let AB be the diameter of a semicircle, C any point on AB, and CD perpendicular to it, and let semicircles be described within the first semicircle and having AC, CB as diameters. Then if two circles be drawn touching CD on different sides and each touching two of the semicircles, the circles so drawn will be equal."
- ^ Boas، Harold P. (2006). "Reflections on the Arbelos". الرياضيات الأمريكية الشهرية. ج. 113 ع. 3: 241. DOI:10.1080/00029890.2006.11920301. مؤرشف من الأصل في 2022-03-20.
The source for the claim that Archimedes studied and named the arbelos is the Book of Lemmas, also known as the Liber assumptorum from the title of the seventeenth century Latin translation of the ninth-century Arabic translation of the lost Greek original. Although this collection of fifteen propositions is included in standard editions of the works of Archimedes, the editors acknowledge that the author of the Book of Lemmas was not Archimedes but rather some anonymous later compiler, who indeed refers to Archimedes in the third person
- ^ Weisstein, Eric W. ""Archimedes' Circles." From MathWorld—A Wolfram Web Resource". مؤرشف من الأصل في 2021-09-04. اطلع عليه بتاريخ 2008-04-10. وسم
<ref>غير صالح؛ الاسم "wolframArbelos" معرف أكثر من مرة بمحتويات مختلفة. - ^ Floor van Lamoen (2014), A catalog of over fifty Archimedean circles. Online document, accessed on 2014-10-08. نسخة محفوظة 10 أبريل 2021 على موقع واي باك مشين.
- ^ Floor van Lamoen (2014), Circles (A61a) and (A61b): Dao pair. Online document, accessed on 2014-10-08. نسخة محفوظة 25 نوفمبر 2020 على موقع واي باك مشين.
- ^ Weisstein, Eric W. ""Archimedes' Circles." From MathWorld—A Wolfram Web Resource". مؤرشف من الأصل في 2022-07-17. اطلع عليه بتاريخ 2008-04-10.Weisstein, Eric W. ""Archimedes' Circles." From MathWorld—A Wolfram Web Resource". Retrieved 2008-04-10.
علامة <ref> بالاسم " archBLprop5 " المحددة في مجموعة <references> " " لا تحتوي على محتوى.
علامة <ref> بالاسم " lamoenCat " المحددة في مجموعة <references> " " لا تحتوي على محتوى.
علامة <ref> بالاسم " lamoenDao " المحددة في مجموعة <references> " " لا تحتوي على محتوى.
| دائرتان توأم في المشاريع الشقيقة: | |