خوارزمية كروسكال

خوارزمية كروسكال

توضيح خوارزمية كروسكال

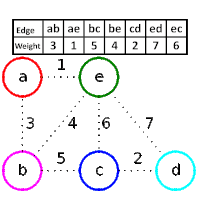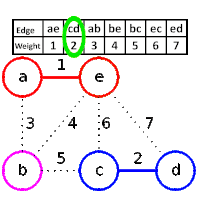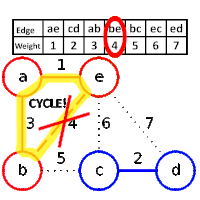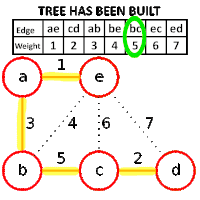
خوارزمية كروسكال (بالإنجليزية: Kruskal Algorithm)‏ هي خوارزمية لإيجاد الطريق ذي الوزن الأقل أو الأقل كلفة، وهي خوارزمية شرهة في نظرية المخططات حيث تجد الطريق الأقل وزن لمخطط متصل موزون، بإضافة الكلفة في كل مرحلة، وهذا يعني أنها توجد المجموعات الجزئية التي تحتوي على الخط الواصل بين عقدتين الذي يكون الشجرة التي تحتوي على جميع العقد، حيث يتم تقليل المجموع الكلي لأوزان الخطوط الواصلة بين العقد في هذه الشجرة لأقل ما يمكن. إذا كان المخطط غير متصل سيقوم بإيجاد الشجرة التي تحتوي على اقل كلفة لكل شجرة في الغابة.

ظهرت هذه الخوارزمية لأول مرة في وقائع المجتمع الأمريكي للرياضيين عام 1956 وكتبها جوزيف كروسكال.

وصف

1- صناعة غابة f تحتوي على مجموعة من الأشجار حيث كل عقدة عبارة عن شجرة منفصلة

2- صناعة مجموعة s تحتوي على كل الخطوط الواصلة بين العقد

3- طالما s ليست فارغة وf ليست ممتدة

        • احذف الخط ذو الأقل وزن

        • إذا كان الخط المحذوف يوصل بين شجرتين مختلفتين إذًا تضاف إلى الغابة f ويتم دمج الشجرتين في شجرة واحدة

عند اختتام الخوارزمية، تكون الغابة تحتوي على الشجرة ذات الطريق الأقل كلفة في المخطط.

السودوكود

الرمز التالي مكتوب مكتوب بهيكلة المجموعة المنفصلة:

KRUSKAL(G):
1 A = ∅
2 foreach v ∈ G.V:
3 MAKE-SET(v)
4 foreach (u, v) in G.E ordered by weight(u, v), increasing:
5 if FIND-SET(u) ≠ FIND-SET(v):
6 A = A ∪ {(u, v)}
7 UNION(u, v)
8 return A

التعقيد

إذا فرضنا E عدد الخطوط الواصلة بين العقد و v هو عدد العقد حيث من الممكن ان تعمل خوارزمية كروسكال بElogE من المرات أو ما يكافئ O(ElogV) مع هيكلة بيانات بسيطة وهي متكافئة لسببين رأيسيين هما: • E على الأكثر ستصل ل V^2 ووهذا يعني انها O(logv) • كل عقدة معزولة هي عنصر منفصل من الغابة فإذا تجاهلنا العقدة المعزولة فان V<=2E يمكننا الوصول إلى هذا إذا تتبعنا هذه الخطوات: الأولى ترتيب الخطوط الواصلة بين العقد حسب وزنها بتعقيد يساوي O(ElogE) وهذا يتيح لعملية الحذف بحذ الخط ذو الأقل وزن بوقت ثابت ثم نستخدم هيكلة المجموعات المنفصلة (الاتحاد والإيجاد) ونحتاج هنا لO(V) من العمليات.

سواء كانت الخطوط مرتبة ام لم تكن مرتبة وسيتم ترتيبها بوقت ينمو خطيًا على سبيل المثال ترتيب راديكس، كما يمكن استخدام هيكلة مجموعات منفصلة معقدة أكثر لتشغيل الخوارزمية ب O(E α(V)) مرة.

مثال

Image	Description
	AD و CE هما الأقل وزنًا بوزن 5 لذلك تم اختيار AD بشكل عشوائي
	الان CE هي الأقصر ولا تكون دائرة لذلك تم اختيارها.
	الخط الأقل وزن التالي هو DF بوزن 6.
	هناك طريقين بنفس الوزن 7 لذلك تم اختيار AB كما تم تعليم DB بالأحمر لأن هناك طريق بين B و D لذلك كان سيكون هناك دائرة إذا تم اخيار DB
	سيتم تحديد BE حيث هو الاقل وزن من الطرق التي لم يتم ختيارها اما BC وDE وEF تم تحديهما بالأحمر لأنها كانت ستصنع دوائر
	وفي النهاية سيتم اختيار الطريق EG

اثبات صحة الخوارزمية

اثبات صحة الخوارزمية ينقسم إلى قسمين الأول اثبات انها شجرة امتداد وثاني انها تملك الطريق الأقل وزنًا

الشجرة الممتدة

لنفرض ان P مخطط موزون وموصول ولنفرض ان Y مخطط جزئي من P صنعت عن طريق الخوارزمية. Y لا يمكن ان تحتوي على دائرة تكون في شجرة جزئية لا في شجرتين مختلقتين كما أن Y لا يمكن ان تكون منفصلة لأن الخط الواصل بين عقدتين يتم اضافته عبر الخوارزمية مما يعني انها شجرة ممتدة

امتلاك اقل وزن

سنثبت ان فرضيتنا صحيحة عبر الإستقراء: إذا كانت F مجموعة من الخطوط الواصلة بين العقد مختارة في أحد المراحل من الخوارزمية إذا هنا بعض من الشجر الممتد الذي يحتوي على F

•P صحيحة في البداية عندما تكون F فارغة: أي شجرة ممتدة تملك اقل وزن تخضع لهذا لأن كل مخطط موزون متصل يحتي على شجرة ممتدة تملك اقل وزن في المخطط

• لنفرض الآن ان P صحيحة ل بعض الخطوط الواصلة بين العقد اللا نهائية ولنفرض ان T شجرة ممتدة تمتلك الوزن الأقل وتحتوي على F إذا كان الخط التالي المختار ايضًا في T إذا P صحيحة إذا عندما تكون F+e اما إذا كان T+e يحتوي على دائرة C وهناك خط اخر f موجود في C لكن ليس موجود في F فإن T-f+e شجرة وهي تملك وزن مساوي لوزن T وبما أن T تملك الوزن الأقل وf لا يمكن ان يكون أقل من e والا كانت اختارت الخوارزمية f بدلا من e إذا T-f+e هي شجرة ممتدة تحتوي على أقل وزن في المخطط

• لهذا السبب جوهر الإستقراء P تثبت عندما تكون F شجرة ممتدة بحيق تكون F الاحتمال الوحيد لتكون شجرة ممتدة تملك الوزن الأقل

مراجع

↑ 1.0 1.1 Cormen, Thomas; Charles E Leiserson, Ronald L Rivest, Clifford Stein (2009). Introduction To Algorithms (Third ed.). MIT Press. p. 631. ISBN 0-262-25810-2. 2.↑ Kruskal, J. B. (1956). "On the shortest spanning subtree of a graph and the traveling salesman problem". Proceedings of the American Mathematical Society 7: 48–50. doi:10.1090/S0002-9939-1956-0078686-7. JSTOR 2033241. Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0-262-03293-7. Section 23.2: The algorithms of Kruskal and Prim, pp. 567–574. Michael T. Goodrich and Roberto Tamassia. Data Structures and Algorithms in Java, Fourth Edition. John Wiley & Sons, Inc., 2006. ISBN 0-471-73884-0. Section 13.7.1: Kruskal's Algorithm, pp. 632..