تأثير زيمان

تأثير زيمان هو ظاهرة انشقاق خطوط الطيف لمصدر تحت تأثير مجال مغناطيسي ثابت إلى عدة خطوط؛ أي أن تأثير زيمان يشق خطوط الطيف إلى خطوط متوازية عندما يوضع مصدر الضوء في مجال مغناطيسي شديد . وهو تاثير يرجع إلى العالم الهولندي بيتر زيمان الذي اكتشف هذه الظاهرة في عام 1896م. وهذا التأثير مشابه لتأثير آخر يسمى تأثير شتارك وهو انشقاق خطوط الطيف إلى عدة خطوط في حالة تعرض مصدر الضوء إلى مجال كهربائي.

ويستخدم تأثير زيمان في تطبيقات عديدة في مطياف الرنين المغناطيسي، ومطياف رنين الدوران المغزلي للإلكترون، وفي التصوير بالرنين المغناطيسي (MRI). وكثيرا ما يستخدم تأثير زيمان للتعيين الدقيق للأطياف الامتصاصية للعناصر. وفي حالة قياس خطوط الطيف الامتصاصي، يسمى بتأثير زيمان العكسي.

ظهور إنشقاق لخطوط الطيف عندما تتأثر بمجال مغناطيسي خارجي (أي عندما تكون B لاتساوي صفرا.)

مقدمة

توجد في الذرات توزيعات مختلفة للإلكترونات لها طاقة محددة ؛ تلك التوزيعات تشغل مستويات للطاقة مختلفة. في الحالة المستقرة للذرة (الذرة غير مثارة) تشغل الإلكترونات مستويات قاعية ground state في الذرة تتميز بقلة طاقتها . وعند إثارة الذرة مثلا بواسطة الحرارة لان بعض الإلكترونات تترك حالها القاعية وترتفع إلى مستوى طاقة أعلى. لذلك تظهر بعد ذلك عدة قفزات للإلكترونات من مدارات أعلى للطاقة إلى مدار أقل طاقة، تظهر متمثلة في خطوط في طيفها. وفي وجود مجال مغناطيسي خارجي تنشق تلك الخطوط، حيث يتأثر كل إلكترون في الذرة بالمجال المغناطيسي الخارجي بطريقة مختلفة بحسب، هل عزمه المغناطيسي موازيا للمجال المغناطيسي الخارجي أم أنه معكوس الاتجاه . هذا يعتمد على عدد الكم المغزلي له . فالأعداد المغزلية المختلفة تُعبر عن حالات طاقة مختلفة . وعل الرغم من أنها فروقاً طفيفة في الطاقة، إلا أنها تؤدي إلى انقسام في خط الطيف ً تحت تأثير المجال المغناطيسي، فبدلا من ان يظهر انتقال إلكترون بين مستويين معينين للطاقة في هيئة خط واحد في الطيف، فهو ينشق إلى خطين أو ثلاثة خطوط .

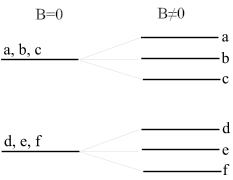
وطبقا للرسم التوضيحي، تتسم مستويات الطاقة للإلكترونات a، b، c بأن لها نفس الطاقة في غياب مجال مغناطيسي خارجي. كما ينطبق هذا أيضا علي مستويات الطاقة d, e, f التي توجد في حالة طاقة محددة منخفضة عن حالة a، b، c. وفي وجود المجال المغناطيسي تنشق مستويات الطاقة، وينتج عن ذلك أنه بينما كان يظهر لنا الانتقال من a، b، c إلى d، e، f في خط واحد، يصبح لدينا عدة خطوط بسبب وجود عدد من الانتقالات الممكنة بين a، b، c إلى المستويات d, e, f. ولكن لا يمكن للإلكترون القفز (الانتقال) إلى جميع المستويات المنخفضة d، e، f بلا إستثناء، وإنما هو محكوم بقفزات مسموحة وأخرى غير مسموحة، بحسب قاعدة لذلك (انظر أسفله).

ونظرا لأن مقدار الانشقاق في خطوط الطيف تتناسب تناسباً طرديا ً مع شدة المجال المغناطيسي الخارجي، يستخدم علماء الفلك تـأثير زيمان في قياس المجالات المغناطيسية للشـمس والنجوم الأخرى ومقارنتها؛ وذلك عن طريق قياس انشقاق خطوط طيف الشمس التي نرصدها ونحللها.

مثال : الانتقال الخاص بخط لايمان-ألفا في الهيدروجين

يشتمل الانتقالان المنتميان لخط لايمان ألفا في طيف الهيدروجين على الانتقالات التالية للإلكترون بين الأغلفة الذرية:

$2P_{1/2}\to 1S_{1/2}$ و

$2P_{3/2}\to 1S_{1/2}$.

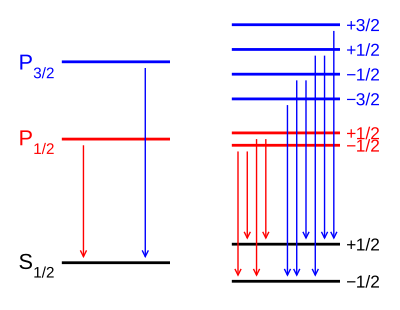
وطبقا للشكل، يمثل الرسم على اليسار حالة إلكترون ذرة الهيدروجين في عدم وجود مجال مغناطيسي خارجي . في تلك الحالة يمكن للإلكترون أن يشغل مستويات الطاقة التالية : $1S_{1/2}$ أو $2P_{1/2}$ أو $2P_{3/2}$ . وبالتالي يوجد انتقالين للإلكترون من أعلى إلى أسفل إلى المستوي $1S_{1/2}$ لكي تصل الذرة لحالة الاستقرار، أي تصدر الذرة خلال الانتقالين خطي الطيف :$2P_{1/2}\to 1S_{1/2}$ و $2P_{3/2}\to 1S_{1/2}$ كما هو مبين في الشكل (يسار).

أما في حالة وجود مجال مغناطيسي خارجي فتنشق كل من الحالتين الكموميتين 1S_1/2 و 2P_1/2 إلى مستويين اثنين وهما: $m_j=1/2,-1/2$ ، حيث $m_j$ عدد الكم المغناطيسي (وهو يحتوي في الحالة S على الدوران المغزلى للإلكترون فقط) ؛ وفي نفس الوقت تنشق الحالة 2P_3/2 إلى أربعة مستويات للطاقة (أزرق) ، وهي :

$m_j=3/2;1/2;-1/2;-3/2$

حيث أن عدد الكم المداري للإلكترون l=1 في المدار P ؛ و$m_j$ للإلكترون وعدده المغزلي 1/2 .

وكما نرى يتشابك عزم المدار الذي يبلغ 1 مع العزم المغزلي الذي يبلغ 1/2 ، وتنتج من احتمالات التباديل والتوافيق بينهم الأربعة مستويات المبينة بالشكل (أزرق) ، مع الاخذ في الاعتبار الاتجاهات الكمومية إلى أعلى وإلى أسفل.

وعند انتقال الإلكترون من اعلى إلى أسفل للوصول إلى حالة الاستقرار، نجد تعدد خطوط الطيف الصادرة عن كل انتقال من مستوى طاقة عالي إلى مستوى طاقة تحته.

ونلاحظ هنا :

• أن اتساع الانشقاق بين مستويات الطاقة مختلف باختلاف قيمة $m_j$ إذ أن مقدار الانشقاق يتناسب مع شدة تآثر الإلكترون مع المجال المغناطيسي الخارجي، والذي يحدده معامل لاندي (g - factor) والذي يعتمد على $m_j$.
• أنه ليست جميع انتقالات الإلكترون من المستويات العليا إلى المستويات السفلى مسموح بها. فهناك انتقالات مسموحة، وأخرى غير مسموحة، وتوجد قاعدة تتحكم في تصرف الإلكترون في هذا المجال.

في الرصد الفلكي

زيادة اتساع خط الامتصاص في طيف الشمس (الخط الرأسي) بالقرب من بقعة شمسية (يشتد فيها المجال المغناطيسي ، يسار). وهو مبين مضخما لزيادة التوضيح (يمين).

عن طريق رصد الشمس استطاع «جورج هيل» اكنشاف وجود مجالات مغناطيسية شديدة في البقع الشمسية . هذا ما تبينه الصورة إلى اليسار عبر أحد البقع الشمسية. على طول خط الطيف يزداد عرضا في منطقة البقعة الشمسية . ويظهر الخط خارج هذه البقعة كخط واضح دقيق .

المجال المغناطيسي على الشمس ;B يبلغ 0,1 تسلا يتسبب في انشقال خطوط الطيف :

$\mathrm{\Delta }E={\mu }_{\mathrm{B}}\cdot B=5\cdot 10^{-6}$ إلكترون فولط

وهو يتفاعل مع مغنطون بور للإلكترون ${\mu }_{\mathrm{B}}$.

الانشقاق الذي يحدث لخطوط الطيف يكون صغيرا جدا ويحتاج إلى مطياف دقيق يكون تباينه أدق من 10⁻⁴ لمشاهدته.

التعبير النظري

مجموع هاميلتونيان للذرة في مجال مغناطيسي

$H=H_0+V_M,$

حيث $H_0$رابطة هاملتون في الذرة و $V_M$ الاضطراب المجال المغناطيسي

$V_M=-\overrightarrow{\mu }\cdot \overrightarrow{B},$

$\overrightarrow{\mu }$المغناطيس اللحظي للذرة , يتكون من جزء الكتروني وجزء نووي، وبشكل عام هذا الرمز يرمز لعدة مجالات مغناطيسية صغيرة، مثل

$\overrightarrow{\mu }=-{\mu }_{B}g\overrightarrow{J}/\hslash ,$

${\mu }_B$ مغناطيس بور و j الزخم الكلي (مجموع اللف المداري Lواللف المغزلي S ) و $g$ معامل لاندي , تعطى نسبة الجيرومغناطيسية :$\overrightarrow{\mu }=-{\mu }_B(g_l\overrightarrow{L}+g_s\overrightarrow{S})/\hslash ,$

حيث $g_l=1$ و $g_s\approx 2.0023192$

وفي حالة L-S مرتبطان:

$g\overrightarrow{J}=⟨{\sum }_i(g_l\overrightarrow{l_i}+g_s\overrightarrow{s_i})⟩=⟨(g_l\overrightarrow{L}+g_s\overrightarrow{S})⟩,$

إذا كان شرط التفاعل V_Mصغير يتم التعامل مع المفعول على أنه مفعول زيمان العادي، ولكن في مفعول باشن باك V_M تكون قيمة الاضطراب كبيرة بشكل ملحوظ (لكن H₀ تبقى صغيرة كما هي ) في المجالات المغناطيسية القوية ترتفع قيمة H0وتخرج الذرة من نطاقها المألوف ويظهر أثر مستويات لانداو.

المجال الضعيف (أثر زيمان)

تفاعل اللف المغزلي- المداري داخل الذرة أكبر من تأثير المجال المغناطيسي الخارجي، يحسب متوسط إسقاط متجه اللف المغزلي على الزخم الزاوي الكليJ

${\overrightarrow{S}}_{avg}=\frac{(\overrightarrow{S}\cdot \overrightarrow{J})}{J^2}\overrightarrow{J}$

ومتوسط متجه اللف المداري

${\overrightarrow{L}}_{avg}=\frac{(\overrightarrow{L}\cdot \overrightarrow{J})}{J^2}\overrightarrow{J}.$

بالتالي

$⟨V_M⟩=\frac{{\mu }_B}{\hslash }\overrightarrow{J}(g_L\frac{\overrightarrow{L}\cdot \overrightarrow{J}}{J^2}+g_S\frac{\overrightarrow{S}\cdot \overrightarrow{J}}{J^2})\cdot \overrightarrow{B}.$

وباستخدام $\overrightarrow{L}=\overrightarrow{J}-\overrightarrow{S}$ وتربيع الطرفين

$\overrightarrow{S}\cdot \overrightarrow{J}=\frac{1}{2}(J^2+S^2-L^2)=\frac{{\hslash }^2}{2}[j(j+1)-l(l+1)+s(s+1)],$

وباستخدام $\overrightarrow{S}=\overrightarrow{J}-\overrightarrow{L}$ وتربيع الطرفين

$\overrightarrow{L}\cdot \overrightarrow{J}=\frac{1}{2}(J^2-S^2+L^2)=\frac{{\hslash }^2}{2}[j(j+1)+l(l+1)-s(s+1)].$

والجمع ووضع $J_z=\hslash m_j$ نحصل على الطاقة المغناطيسية المحتملة للذرة عند تطبيق مجال مغناطيسي خارجي :

$V_M={\mu }_{B}B{m}_j[g_L\frac{j(j+1)+l(l+1)-s(s+1)}{2j(j+1)}+g_S\frac{j(j+1)-l(l+1)+s(s+1)}{2j(j+1)}],$

الكمية بين قوسين هي متجه لاندي للذرة ($g_L=1$ و $g_S\approx 2$ )) m_j المركبة باتجاه Z الزخم الزاوي الكلي ويكون الإلكترون المفرد في المدار s = 1 / 2 .

مثال : انتقال ليمان – الفا في الهيدروجين

الانتقالات الممكنة

$2P_{1/2}\to 1S_{1/2}$ and $2P_{3/2}\to 1S_{1/2}.$

في المجال المغناطيسي الضعيف ينقسم 1S1/2 و 2P1/2إلى مستويين (mj = 1 / 2, − 1 / 2) والمستوى 2P3/2ينقسم إلى أربع مستويات (mj = 3 / 2,1 / 2, − 1 / 2, − 3 / 2), متجه لاندي للمستويات الثلاثة هو :

gJ = 2 for 1S1 / 2 (j=1/2, l=0)
gJ = 2 / 3 for 2P1 / 2 (j=1/2, l=1)
gJ = 4 / 3 for 2P3 / 2 (j=3/2, l=1).
ملاحظة : طاقة تقسيم المستويات تختلف من مستوى لآخر وذلك لاختلاف قيمة معامل لاندي

المجال القوي (مفعول باشن باك )

عندما اضطراب المجال المغناطيسي يتجاوز بشكل ملحوظ تفاعل اللف المداري – المغزلي نفرض أن H₀,S] = 0] فيسمح هذا الفرض توقع قيمة L_z و Szبسهولة ممايسمح بتقييم مستوى $|A⟩$:

$⟨A\left|(H_0+\frac{B_z{\mu }_B}{\hslash }(L_z+g_s{S}_z))\right|A⟩=E_0+B_z{\mu }_B(m_l+g_s{m}_s).$

نجد من الصيغة أن اقتران اللف المداري والمغزلي ليس له أثر يذكر مقارنة بأثر المجال المغناطيسي ml و msأعداد كمية جيدة مع قاعدة الانتقاء لتحولات ثنائي القطبالكهربي

$\mathrm{\Delta }s=0,\mathrm{\Delta }{m}_s=0,\mathrm{\Delta }l=\pm 1,\mathrm{\Delta }{m}_l=0,\pm 1$
ويمكن حساب طاقة المستويات الإلكترونية من $\mathrm{\Delta }E=B{\mu }_B\mathrm{\Delta }{m}_l$

أنظر أيضا ً

• ذرة
• تأثير شتارك
• طاقة زيمان
• تجربة شتيرن-غيرلاخ