انحدار خطي بسيط

الانحدار الخطي البسيط هو حساب المربعات الصغرى من نموذج الانحدار الخطي مع متغير تفسيري واحد.^[1]^[2]^[3] وبعبارة أخرى، الانحدار الخطي البسيط هو خط مستقيم يمر بمجموعة من النقاط بطريقة تجعل مجموع مربع النقط المتبقية من النموذج (أي، المسافات الرأسية بين النقطة المتبقية والخط) أقل ما يمكن. هذا يشير الي حقيقة أن الانحدار هو واحد من أبسط الأساليب المستخدمة في مجال الإحصاء حيث أن ميل الخط يساوي العلاقة بين y و x مصححة بنسبة الانحرافات المعيارية لهذه المتغيرات. نقطة تقاطع الخط مع محور الصادات هي مركز كتلة نقاط البيانات (x, y). توجد طرق انحدار أخرى بجانب المربعات الصغرى البسيطة (انظر الانحدار الخطي). علي وجه الخصوص، عندما يريد شخص أن يقوم بفعل الانحدار عن طريق العين فانه يميل عادة الي رسم خط حاد قليلا ويكون قريبا من ذلك الذي ينتج من طريقة أقل مربعات كليه. يحدث هذا لأنه طبيعي أكثر لعقل الإنسان ملاحظة المسافات المتعامدة علي خط الانحدار بدلا من تلك الراسية كما يحدث في طريقة المربعات الصغرى.

عمل خط الانحدار

افترض ان لديك عدد n من النقاط {(X_i,Y_i),i=1,2,.....n} فان الدالة التي تصف Y و X هي: y_i = α + β x_i + ε_i والهدف هو ايجاد معادلة الخط المستقيم y = α + β x التي تعطي أفضل تمثيل للنقاط. هنا الأفضل يعرف بأنه طريقة المربعات الصغيرة: الخط الذي يقلل مجموع مربعات المتبقيات لنموذج الانحدار الخطي. وبعبارة أخرى، α (نقطة التقاطع مع محور y) و β (الميل) يشاركوا في حل مشكلة التقليل التالية: $Find \min_{α, β} Q (α, β), for Q (α, β) = \sum_{i = 1}^{n} ε_{i}^{2} = \sum_{i = 1}^{n} (y_{i} - α - β x_{i})^{2}$

باستخدام الحساب هندسة المساحات الداخلية للشكل أو التوسع البسيط للحصول علي معادلة من الدرجة الثانية في α و β ، فإنه من الممكن ايجاد قيم α و β التي تقلل الدالة كالتالي:

 $\begin{array}{l} \hat{β} & = \frac{\sum_{i = 1}^{n} (x_{i} - \bar{x}) (y_{i} - \bar{y})}{\sum_{i = 1}^{n} (x_{i} - \bar{x})^{2}} \\ [6 p t] & = \frac{\sum_{i = 1}^{n} x_{i} y_{i} - \frac{1}{n} \sum_{i = 1}^{n} x_{i} \sum_{j = 1}^{n} y_{j}}{\sum_{i = 1}^{n} x_{i}^{2} - \frac{1}{n} (\sum_{i = 1}^{n} x_{i})^{2}} \\ [6 p t] & = \frac{\overline{x y} - \bar{x} \bar{y}}{\overline{x^{2}} - {\bar{x}}^{2}} \\ = \frac{C o v [x, y]}{V a r [x]} \\ = r_{x y} \frac{s_{y}}{s_{x}}, \\ [6 p t] \hat{α} & = \bar{y} - \hat{β} \bar{x}, \end{array}$

حيث $r xy$ هو معامل الارتباط بين x و y

$s x$ هو الانحراف المعياري ل x

$s y$ هو الانحراف المعياري ل y الخط الأفقي علي فوق الكمية يعبر عن المتوسط. فعلى سبيل المثال: $\overline{x y} = \frac{1}{n} \sum_{i = 1}^{n} x_{i} y_{i} .$

بالتعويض بالمعادلة السابقة في $f = \hat{α} + \hat{β} x,$ يؤدي ذلك الي: $\frac{f - \bar{y}}{s_{y}} = r_{x y} \frac{x - \bar{x}}{s_{x}}$

و هذا يدل علي الدور الذي يقوم به $r xy$ في خط الانحدار لنقط البيانات. وفي بعض الأحيان يكون من المفيد حساب $r xy$ من البيانات بشكل مستقل باستخدام المعادلة التالية:

$r_{x y} = \frac{\overline{x y} - \bar{x} \bar{y}}{\sqrt{(\overline{x^{2}} - {\bar{x}}^{2}) (\overline{y^{2}} - {\bar{y}}^{2})}}$

معامل التحديد (R تربيع) يساوي $r_{x y}^{2}$ عندما يكون النموذج خطي وبه متغير مستقل واحد. انظر نموذج معامل الارتباط لتفاصيل أكثر

انحدار خطي بدون جزء التقاطع

في بعض الأحيان، يعتبر الناس نموذج الانحدار الخطي البسيط دون جزء التقاطع $y = βx$ في مثل هذه الحالة، تقدير OLS لايجاد β يبسط ل $\hat{β} = \frac{\sum_{i = 1}^{n} x_{i} y_{i}}{\sum_{i = 1}^{n} x_{i}^{2}} = \frac{\overline{x y}}{\overline{x^{2}}}$

ويصبح معامل ارتباط العينة: $r_{x y} = \frac{\overline{x y}}{\sqrt{(\overline{x^{2}}) (\overline{y^{2}})}}$

خصائص عددية

الخط يمر عبر نقطة مركز الكتلة $(x, y)$
مجموع المتبقيات يساوي صفر إذا وجد ثابت في النموذج: $\sum_{i = 1}^{n} {\hat{ε}}_{i} = 0 .$
التركيبة الخطية للمتبقيات، في حالة المعاملات هي قيم x، تساوي صفر: $\sum_{i = 1}^{n} x_{i} {\hat{ε}}_{i} = 0 .$

خصائص ايجاد نموذج

وصف الخصائص الإحصائية للمقدرات من الانحدار الخطي البسيط يتطلب استخدام نموذج احصائي. التالي يعتمد علي افتراض صحة النموذج في حالة أن التقديرات مثالية. ومن الممكن أيضا لحساب الخصائص تحت قيود افتراضات أخرى، مثل عدم التجانس، ولكن يتم مناقشة ذلك في أماكن أخرى.

عدم التحيز

حساب $\hat{α}$ و $\hat{β}$ هي منحازة وهذا يتطلب أن نفسر المقدرات كمتغيرات عشوائية وعلينا أن نفترض أن لكل قيمة ل x القيمة المقابلة لها في y تنتج كنتيجة متوسطة $α + βx$ بالإضافة الي قيمة متغير عشوائي اضافي ε يسمي الخطأ. هذا الخطأ يجب أن يساوي صفر عند حساب المتوسط لكل قيمة ل x وتحت هذا التفسير، تقدير المربعات الصغيرة $\hat{α}$ و $\hat{β}$ سوف يكونوا متغيرات عشوائية وسوف تحسب القيم الحقيقية ل α و β بدون تحيز.

فترات التأكيد

المعادلات المعطاة في الجزء السابق تمكننا من حساب تقديرات النقط ل α و β وهم معاملات خط الانحدار لمجموعة معينة من البيانات. ومع ذلك، هذه المعادلات لا تخبرنا مدي الدقة في التقديرات أي كم المقدرات $\hat{α}$ و $\hat{β}$ تختلف من نموذج لاخر لحجم العينة المحدد. لذا وضع ما يسمي فترات التأكيد لتعطي مجموعة معقولة من القيم التي يمكن تقديرها إذا كررت التجربة عدد هائل من المرات. الطريقة التقليدية لحساب فترات التأكيد لمعاملات الانحدار الخطي تعتمد علي فرض الثبات الذي له ما يبرره إذا ما:

الخطأ في الانحدار كان متوزع طبيعي (ما يسمي افتراض الانحدار الكلاسيكي)
عدد الملاحظات n كان كبير بشكل كافي في حالة المقدرات كانت موزعة تقريبا بشكل طبيعي

هذا ما يبرر الحالة الأخيرة من نظرية حدود المركز

افتراض الوضع الطبيعي

في ظل الافتراض الأول أعلاه، الذي من طبيعته وجود خطأ، تقدير معامل الميل سوف يوزع بشكل طبيعي بمتوسط β وتباين $σ^{2} / \sum (x_{i} - \bar{x})^{2},$ حيث $σ 2$ هو الفرق في الخطأ (انظر البراهين التي تنطوي علي المربعات الصغري). في نفس الوقت، مجموع مربع المتبقيات Q يوزع بالتناسب مع $χ 2$ بعدد درجات حرية n-2 وبشكل مستقل عن $\hat{β} .$ وهذا يسمح لنا بعمل احصائية t. $t = \frac{\hat{β} - β}{s_{\hat{β}}} \sim t_{n - 2},$

حيث

$s_{\hat{β}} = \sqrt{\frac{\frac{1}{n - 2} \sum_{i = 1}^{n} {\hat{ε}}_{i}^{2}}{\sum_{i = 1}^{n} (x_{i} - \bar{x})^{2}}}$

هو الخطأ المعياري للمقدر احصائية t لديها توزيع t للطلاب بعدد n-2 درجة حرية وباستخدامها نستطيع تكوين فترة تأكيد ل β:

$β \in [\hat{β} - s_{\hat{β}} t_{n - 2}^{*}, \hat{β} + s_{\hat{β}} t_{n - 2}^{*}],$

في مستوي التأكيد $(1- γ)$ حيث $t_{n - 2}^{*}$ هي $(1- γ / 2)$ -th من توزيع $t n -2$ على سبيل المثال، إذا $γ = 0.05$ ثم مستوي التأكيد 95% وبالمثل، فترة التأكيد لمعامل الاعتراض $α$ يعطي ب

$α \in [\hat{α} - s_{\hat{α}} t_{n - 2}^{*}, \hat{α} + s_{\hat{α}} t_{n - 2}^{*}],$

في مستوي التأكيد $(1- γ)$ حيث

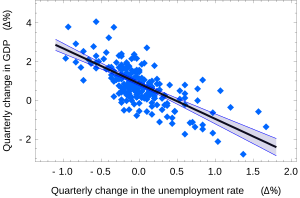
$s_{\hat{α}} = s_{\hat{β}} \sqrt{\frac{1}{n} \sum_{i = 1}^{n} x_{i}^{2}} = \sqrt{\frac{1}{n (n - 2)} (\sum_{j = 1}^{n} {\hat{ε}}_{j}^{2}) \frac{\sum_{i = 1}^{n} x_{i}^{2}}{\sum_{i = 1}^{n} (x_{i} - \bar{x})^{2}}}$

فترة التأكيد ل $α$ و $β$ تعطينا الفكرة الرئيسية حيث معاملات الانحدار من الأرجح أن تكون. على سبيل المثال، في قانون Okun الانحدار ظاهر في بداية المقال النقط المقدرة هي $\hat{α} = 0.859, \hat{β} = - 1.817 .$

و فترة التأكيد لهذه المقدرات 95%: $α \in [0.76, 0.96], β \in [- 2.06, - 1.58] .$

من أجل تمثيل هذه المعلومات بيانيا في شكل فترات تأكيد ول خط الانحدار فعلي الشخص أن يمضي بحذر وحساب التوزيع المشترك للمقدرات. ويمكن أن تظهر أنه في فترة التأكيد (1−γ) رابطة التأكيد تأخذ شكل قطع زائد يعطي بالمعادلة:

$\hat{y} |_{x = ξ} \in [\hat{α} + \hat{β} ξ \pm t_{n - 2}^{*} \sqrt{(\frac{1}{n - 2} \sum {\hat{ε}}_{i}^{2}) \cdot (\frac{1}{n} + \frac{(ξ - \bar{x})^{2}}{\sum (x_{i} - \bar{x})^{2}})}] .$

الافتراضات التقريبية

الافتراض الثاني البديل ينص علي أنه عندما يكون عد النقاط كبير بشكل كاف، وقانون الأعداد الكبيرة ونظرية حدود المركز قابلين للتطبيق، ومن ثم توزيع المقدرات أمر طبيعي تقريبا. تحت هذا الافتراض جميع الصيغ المشتقة في القسم السابق لا تزال سارية المفعول، مع استثناء وحيد وهو أن t*_n−2 لتوزيع t من الطلاب يتم استبداله ب q* من التوزيع الطبيعي القياسي. أحيانا الكسر $1 / n -2$ يتم استبداله ب $1 / n$ في حالة n تكون كبيرة ومثل هذا التغير لا يغير النتائج بشكل ملحوظ.

مثال عددي

هذا المثال يتعلق بمجموعة بيانات من المربعات الصغري العادية. هذه المجموعة تعطي متوسط كتل السيدات كدالة في طولهم في عينة من النساء الأمريكان في عمر 39-30 . وعلى الرغم أن OLS تقول أنه من الأكثر ملائمة عمل انحدار من الدرجة الثانية لهذه البيانات لكن الانحدار الخطي البسيط يمكن تطبيقه هنا بدلا من ذلك.

x_i	1.47	1.50	1.52	1.55	1.57	1.60	1.63	1.65	1.68	1.70	1.73	1.75	1.78	1.80	1.83	Height (m)
y_i	52.21	53.12	54.48	55.84	57.20	58.57	59.93	61.29	63.11	64.47	66.28	68.10	69.92	72.19	74.46	Mass (kg)

يوجد عدد النقاط (n=15) في هذه البيانات ويتم بدأ الحسابات باليد بحساب المجاميع الخمسة التالية:

 $\begin{array}{l} S_{x} = \sum x_{i} = 24.76, S_{y} = \sum y_{i} = 931.17 \\ S_{x x} = \sum x_{i}^{2} = 41.0532, S_{x y} = \sum x_{i} y_{i} = 1548.2453, S_{y y} = \sum y_{i}^{2} = 58498.5439 \end{array}$

هذه الكميات تستخدم لحساب معاملات الانحدار وأخطائهم القياسية

$\begin{array}{l} \hat{β} & = \frac{n S_{x y} - S_{x} S_{y}}{n S_{x x} - S_{x}^{2}} = 61.272 \\ \hat{α} & = \frac{1}{n} S_{y} - \hat{β} \frac{1}{n} S_{x} = - 39.062 \\ s_{ε}^{2} & = \frac{1}{n (n - 2)} (n S_{y y} - S_{y}^{2} - {\hat{β}}^{2} (n S_{x x} - S_{x}^{2})) = 0.5762 \\ s_{β}^{2} & = \frac{n s_{ε}^{2}}{n S_{x x} - S_{x}^{2}} = 3.1539 \\ s_{α}^{2} & = s_{β}^{2} \frac{1}{n} S_{x x} = 8.63185 \end{array}$

0.975 من توزيع t للطلاب ب 13 درجة حرية يكون t^*₁₃=2.1604 وبالتالي 95% فترة تأكيد ل $α$ and $β$ تكون:

$\begin{array}{l} α \in [\hat{α} \mp t_{13}^{*} s_{α}] = [- 45.4, - 32.7] \\ β \in [\hat{β} \mp t_{13}^{*} s_{β}] = [57.4, 65.1] \end{array}$

و يمكن أيضا حساب ناتج معامل تصحيح الارتباط كالتالي:

$\hat{r} = \frac{n S_{x y} - S_{x} S_{y}}{\sqrt{(n S_{x x} - S_{x}^{2}) (n S_{y y} - S_{y}^{2})}} = 0.9945$

هذا المثال يوضح أن الحسابات المعقدة لن تتغلب علي استخدام البيانات المعدة بشكل سيئ. الأطوال أعطت بالبوصة وقد تم تحويلها لأقرب سنتيمتر. ولأن معامل التحويل هو 2.54 فهذا تحويل غير صحيح لأن البوصة الأصلية يمكن استردادها بحوالي (x/0.0254) ومن ثم إعادة تحويلها لمتر. إذا فعلت ذلك تصبح النتئج:

$\hat{β} = 61.6746, \hat{α} = - 39.7468 .$

و بالتالي اختلاف صغير في البيانات لديه تأثير حقيقي

الاشتقاق من متغيرات الانحدار الخطي

نحن نبحث عن $\hat{α}, \hat{β}$ التي تقلل مجموع مربع الخطأ، $\underset{\hat{α}, \hat{β}}{m i n} S S E (\hat{α}, \hat{β})$ التي تعرف كالتالي $S S E (\hat{α}, \hat{β}) = \sum_{i = 1}^{n} {(y_{i} - \hat{α} - \hat{β} x_{i})}^{2}$

لايجاد الأقل نقوم بالاشتقاق الجزئي بالنسبة ل $\hat{α}$ و $\hat{β}$

 $\begin{array}{l} \frac{\partial S S E (\hat{α}, \hat{β})}{\partial \hat{α}} = - 2 \sum_{i = 1}^{n} (y_{i} - \hat{α} - \hat{β} x_{i}) = 0 \end{array}$

\begin{array}{l} \sum_{i = 1}^{n} (y_{i} - \hat{α} - \hat{β} x_{i}) = 0 \end{array}

\begin{array}{l} \sum_{i = 1}^{n} y_{i} = \sum_{i = 1}^{n} \hat{α} + \hat{β} \sum_{i = 1}^{n} x_{i} \end{array}

بضرب الطرفين في $\frac{1}{n}$

$\begin{array}{l} \frac{1}{n} \sum_{i = 1}^{n} y_{i} = \hat{α} \frac{1}{n} \sum_{i = 1}^{n} 1 + \hat{β} \frac{1}{n} \sum_{i = 1}^{n} x_{i} . \end{array}$

نحصل علي:

$\begin{array}{l} \bar{y} = \hat{α} + \hat{β} \bar{x} \end{array}$

قب الاشتقاق الجزئي بالنسبة ل $\hat{β}$ عوض بالنتيجة السابقة ل $\hat{α}$

$\begin{array}{l} \underset{\hat{α}, \hat{β}}{m i n} \sum_{i = 1}^{n} {(y_{i} - (\bar{y} - \hat{β} \bar{x}) - \hat{β} x_{i})}^{2} \end{array}$

\begin{array}{l} \underset{\hat{α}, \hat{β}}{m i n} \sum_{i = 1}^{n} {[(y_{i} - \bar{y}) - \hat{β} (x_{i} - \bar{x})]}^{2} \end{array}

الآن، اشتق جزئيا بالنسبة ل $\hat{β}$ :

$\begin{array}{l} \frac{\partial S S E (\hat{α}, \hat{β})}{\partial \hat{β}} = - 2 \sum_{i = 1}^{n} [(y_{i} - \bar{y}) - \hat{β} (x_{i} - \bar{x})] (x_{i} - \bar{x}) = 0 \end{array}$

\begin{array}{l} \sum_{i = 1}^{n} (y_{i} - \bar{y}) (x_{i} - \bar{x}) - \hat{β} \sum_{i = 1}^{n} {(x_{i} - \bar{x})}^{2} = 0 \end{array}

\begin{array}{l} \hat{β} = \frac{}{} \frac{\sum_{i = 1}^{n} (y_{i} - \bar{y}) (x_{i} - \bar{x})}{\sum_{i = 1}^{n} {(x_{i} - \bar{x})}^{2}} = \frac{C o v (x, y)}{V a r (x)} \end{array}

و في النهاية عوض ب $\hat{β}$ لتحديد $\hat{α}$

$\begin{array}{l} \hat{α} = \bar{y} - \hat{β} \bar{x} \end{array}$

مراجع

^ Lane، David M. Introduction to Statistics (PDF). ص. 462. مؤرشف من الأصل (PDF) في 2019-12-10.
^ "What is Simple Linear Regression?". Pennsylvania State University. مؤرشف من الأصل في 2018-12-19. اطلع عليه بتاريخ 2016-10-17.
^ "Statistical Sampling and Regression: Simple Linear Regression". Columbia University. مؤرشف من الأصل في 2017-12-11. اطلع عليه بتاريخ 2016-10-17. When one independent variable is used in a regression, it is called a simple regression;(...)

في كومنز صور وملفات عن: انحدار خطي بسيط

[1] Lane، David M. Introduction to Statistics (PDF). ص. 462. مؤرشف من الأصل (PDF) في 2019-12-10.

[2] "What is Simple Linear Regression?". Pennsylvania State University. مؤرشف من الأصل في 2018-12-19. اطلع عليه بتاريخ 2016-10-17.

[3] "Statistical Sampling and Regression: Simple Linear Regression". Columbia University. مؤرشف من الأصل في 2017-12-11. اطلع عليه بتاريخ 2016-10-17. When one independent variable is used in a regression, it is called a simple regression;(...)

[1]

[2]

[3]