الرياضيات في مصر القديمة

بردية رند.

ابتكر المصريون القدماء نظامًا للأعداد تساعدهم على تعاملاتهم اليومية، وكذلك كان نظام الضرائب يستلزم تواجد نظام للأعداد وللحساب، حيث كان الفلاحون يعطون جزءاً من محاصيلهم السنوية للقصر الملكي وأجزاءً أخرى للمعبد والكهنة. ولا ننسى التجارة المتداولة بين فراعنة مصر مع البلاد المحيطة . من تلك المعاملات التي بدأت منذ عهد الأسرة الأولى مع فلسطين وسورية ولبنان للحصول على الأخشاب، وكذلك مع العراق والنوبة . وامتدت في عهد الملكة حتشبسوت بل وقبلها أيضاً الحملات التجارية إلى بلاد بونت عند القرن الإفريقي على البحر الأحمر . وكثيرا ما كانت المقايضة تـُدفع بالذهب الذي كان المصريون ينقبون عنه في النوبة وفي سيناء.

• كان تعلم الكتابة والحساب يـُزاول في المعابد . وكانت مهنة الكاتب مهنة مرموقة، وكانت لها درجات تـبدأ بالكاتب البسيط (شس) إلى رئيس كتبة وكان هذا يسمى أمير كتبة (أمير-شس)، وتعلو مراتب الكتاب إلى كاتب البلاط الملكي (شس-نسيط) وكانت أعلي مرتبة هي مرتبة أميـر كتبة البلاط الملكي (أمير-شس-نسيط) . وكان أمير كتبة البلاط الملكي في نفس الوقت مهندسا أو طبيبا أو كلاهما معا، وكان الآباء يشجعون أبناءهم علي التعليم واحتراف مهنة الكاتب، حيث أن الكاتب لا يقوم بالأعمال اليدوية أو الجسدية المرهقة التي يقوم بها العمال . بل كانت مهمة الكاتب حتى البسيط منهم مثلا تسجيل المحصول عندما يقوم الفلاحون بجني المحاصيل، وتسجيل عدد الأبقار والأغنام والثروة الحيوانية والطيور، وحساب النسبة المخصصة للقصر على أساس منسوب مياه النيل في ذلك العام.
• ونظام الأعداد الذي ابتكره المصريون القدماء كان نظامًا عشريًا. فكان رمز الواحد شرطة | والعشرة رمزها ، والمئة رمزها والألف رمزوا له ب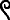 ، كما كان رمز المئة ألف هو الإصبع..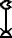 ....، ...وهكذا.

الإله توت تحوت صورة منحوتة على جدار معبد الرامسيوم.

• وكان المصريون القدماء يعتقدون أن الإله توت (Thoth) هو الذي علمهم الحساب والكتابة . وتجد صوره على الأخص في كتاب الموتى، حيث يُصوروه واقفا عند الميزان يوم الحساب في العالم ألآخر، بالقلم ولوح الكتابة في يديه، يدون أعمال الموتى، ويقدم الحساب إلى أوزوريس.
• ومما هو جدير بالذكر أن الكاتب المصري القديم كان يمسك بقلم الكتابة بإصبعين اثنين ويكتب عادة من اليمين إلى اليسار، وكان يبدأ كتابة رسالته قائلا «أكتب إليك بإصبعي الإثنين» .

أعداد

تـُكتب الأربعة 4 هكذا:

.....$4$

وتـُكتب الخمسة عشر 15 هكذا:

.....$15$

وكانوا يكتبون 231 هكذا:

.....$231$

• ولكتابة العدد 4622 على السطر كانوا يكتبوه كالآتي : الرقم الكبير على اليسار والصغير على اليمين، مع العلم بأنهم كانوا يكتبون في العادة من اليمين إلى اليسار، كما نكتب نحن اليوم . وكان اليمين بالنسبة لهم مباركاً ً وطيبا ويسمونه (يمينت) أما اليسار فكانوا لا يحبونه ويعتقدوا أنه مكان الأرواح الشريرة:

.....$4622$

الكسور

استطاع قدماء المصريين أن يبتكروا تركيبة للكسور من الأعداد، وهي طريقة تشابه طريقتنا الحديثة حيث استعملوا رمز الفم وهو ينطق (را) وكتبوا تحته الرقم المعبر عن الكسر . فمثلا، هكذا كانوا يكتبون الكسر العددي 1\3 :

$\frac{1}{3}=$

كما استخدموا رموزا ً خاصة لبعض الأعداد القليلة الكثيرة الاستخدام، مثل النصف 1\2 والثلثين 2\3 والثلاثة أرباع 3\4 :

$\frac{1}{2}=$

$\frac{2}{3}=$

$\frac{3}{4}=$

• وبالإضافة إلى تلك الثلاثة كسور المميزة، ظل المصريون القدامى يعتمدون بصفة أساسية علي الكسر في الهيئة البسيطة 1\س، حيث س يمكن أن تأخذ الأعداد 5، 6 , 7، .....ألخ، مثل :

$\frac{5}{12}=\frac{1}{3}+\frac{1}{12}=$

ولم يتوصلوا لاختصار مثلا (1\5 + 1\5= 2\5)، وكتابة 2\5، بل كانوا يكتبو ن الخـُمسين متجاورين :

$\frac{2}{5}=\frac{1}{5}+\frac{1}{5}=$

ومثال آخر، مثال الثلاثة أخماس :

$\frac{3}{5}=$

أصّروا علي المحافظة على صورة الكسر 1/س، مع مراعاة كتابة الأعداد الصغيرة علي يمين الأعداد الكبيرة :

الكسور وعين حورس

المقالة الرئيسية: عين حورس

استعمل المصريون القدماء مكاييلا لقياس الحبوب والبقول، هذا المعيار كان يـُسمى (حقات) hekat . وكانت الحقات مقسمة للأحجام الآتية : 1\2، 1\4، 1\8، 1\16، 1\32، و1\64 . واستعملوا في كتاباتهم رموزاً مأخوذة عن أجزاء من رمز عين حورس التي كانت مقدسة لديهم، وكانوا عموما ً يستخدمون عين حورس للزينة على شكل القلائد، ولكن الأهم في لبسهم القلائد في صورة عين حورس التي تُسمى (وجات) Ougat، وهي للوقاية من الحسد ومن الكائنات الضارة، والأرواح الشريرة.

صورة لعين حورس وتفاصيل أجزائها وقيمة كل جزء منها الحسابية

• وكما في الصورة استعمل الكاتب المصري هذه الأجزاء من عين حورس لتدوين كميات الحبوب والبقول،

فكان يكتب مثلا كميات من القمح مثلا كالآتي : حقات 1\4 أو حقات 1\16 1\32 .

الجمع عند قدماء المصريين

• كان نظام الأعداد عند قدماء المصريين نظاما عشرياً، لكنهم لم يتوصلوا إلى الصفر . فكان للعشرة رمز خاص بها، وكذلك الحال بالنسبة إلى المئة، والألف، وهكذا . إلا أن نظامهم كان يسهل عمليات الجمع والطرح، وابتكروا طرقا ًً لحسابات الضرب والقسمة . سنبدأ بالجمع :

مثــال : نريد أن نجمع 2322 + 132 = 2454

+

=

والنتيجة كما في السطر الثالث عبارة عن العدد 2454.

الطرح عند قدماء المصريين

طريقة الطرح يسيرة أيضاً مثلها في بساطتها كمثل الجمع.

مثال1: 2322-121 =2201

_

=

ونتيجة عملية الطرح كما نرى 2201 .

مثال2: 5434-3122 =2312

_

=

ونتيجة عملية الطرح كما نرى 2312 .

الضرب عند قدماء المصريين

ابتكر قدماء المصريين طريقة لإجراء العملية الحسابية التي نُعرفها بعملية الضرب وذلك بطريقة استخدام الجمع، وكانت القاعدة الأساسية المتبعة في ذلك هي المضاعفة العددية . وقد عرفنا تلك الطرق التي كانوا يستعملونها في الحساب عن طريق ما وجدناه من آثارهم في هيئة المخطوطات مثل Papyrus de Moscou ومخطوط Papyrus Rhind. ونوضح طريقة المضاعفة المتوالية في عمليات الضرب بالأمثلة ألآتية :

مثال 1: نريد حاصل الضرب 7 . 9 = 63

للحصول على نتيجة حاصل الضرب، يبدأ الكاتب المصري في مضاعفة العدد 7 على التوالي ويبحث عن نتيجة المضروب (8+ 1)، كالآتي :

> 1 ............. 7

	2	..........	14
	4	..........	28
>	8	..........	56
	16	..........	112
	9	..........	63

من خلال مضاعفة 7 يصل عند 7 . 8 = 56، وبعد ذلك يضيف عليها 7 فيحصل على النتيجة، حيث أن 7 + 56 = 63.

مثال 2: نريد حاصل الضرب 59 . 37 = 2183

نبدأ في مضاعفة العدد 59 على التوالي، كالآتي :

* 1 ............. 59

	2	..........	118
*	4	..........	236
	8	..........	472
	16	..........	944
*	32	..........	1888
	37	..........	2183

• من خلال مضاعفة 59 وصلنا أولا ًإلى حاصل ضرب العددين 32 . 59 = 1888 .
• بعد ذلك نضيف عليه حاصل الضرب(انظر الأسطر المعلـّمة): (4 + 1 ). 59 = 236 + 59 = 295 فنحصل على النتيجة 2183.

القسمة عند قدماء المصريين

تعتمد القسمة أيضا على مضاعفة الأعداد على التوالي السابق شرحها مع عمليات الضرب ولكن مع بعض الفروق لمواءمتها للإيفاء بالغرض .

مثال 1: نريد قسمة 264 على 3، أي (264÷3=88)

يبدأ الكاتب المصري القديم بمضاعفة العدد 3 بالخطوات التالية :

	1	..........	3
	2	..........	6
	4	..........	12
>	8	..........	24
>	16	.........	48
	32	.........	96
>	64	..........	192
	88	..........	264

وبتعيين الأعداد المعلـّم عليها بالمؤشر وجمعها يصل إلى النتيجة : 8 + 16 + 64 = 88 .

مثال 2:

يُعتبر مثلنا السابق مثلا بسيطا، فهو يؤدي إلى حاصل قسمة لعدد صحيح لا يحتوي على الكسور.

في مثالنا التالي تؤدي عملية قسمة 212÷6 علي نتيجة تحتوي على الكسور .

نبدأ بمضاعفة العدد 6:

>	1	.... 6
>	2	.... 12
	4	.... 24
	8	.... 48
	16	.... 96
>	32	.... 192
>	1\3	.... 2
	1\3 +35	.... 212

قمنا بمضاعفة العدد 6 حتى وصلنا إلى العدد 192، وبقي فارق بين العددين 212 و192 مقداره 20 فقط . وبمراجعة السطرين الأولين نجد أنهما يأتيان بالعدد 18 ويبقى العدد 2 الذي نجد أنه ثلث العدد 6 .

بهذا يحصل المصري القديم على نتيجة القسمة ويقوم بتدوينها على النحو التالي : 1 + 2 + 32 + 1\3 = 1\3 35

مثال 3:

استطاع الكاتب المصري أيضاً باستعمال طريقة المضاعفة قسمة عدد صغير على عدد كبير .

في المسألة التالية نريد قسمة 4 على 7، أي 4 ÷ 7 = 4/7، فكيف كان يقوم بذلك ?

بمقارنة 4 بالنسبة إلى العدد 7، نجد أن الأربعة أكبر قليلا عن نصف ال 7 . بهذا نجد العضو الأول من الحل، وهو 1/2.

في الخطوة التالية يبدأ المصري القديم بمضاعفة المقام (7) على التوالي كالمعتاد:

	1	.... 7
*	1\2	.... 1\2 3
	1\7	.... 1
*	1\14	.... 1\2
	1\1+14\2	.... 4

وجدنا الحل: فقد وصلنا إلى المقسوم بالكامل وهو العدد 4، ونجمع العددين المطلوبين هنا فنحصل على الحل : 1\14 1\2 .

مثال 4: قسمة 1660 على 33 أي (1660 ÷33):

	1	... 33
1>	2	... 66
	4	... 132
	8	... 264
2>	16	... 528
3>	32	... 1056
4>	1\4	... 1\4 8
5>	1\33	... 1
6>	1\44	... 1\4 1\2
	1\44 + 1\33 + 1\4 + 50	... 1660

ونشرح الطريقة كما يلي : ضاعفنا العدد 33 خمس مرات تباعا ووصلنا إلى العدد 1056 . ونلاحظ أن جمع الأعداد المعلمة 1056 + 528 + 66 = 1650 . والفارق بين 1660 و1650 هو 10 .

ونبدأ البحث عن كسور ال 33 ونجد أن 10 تحتوي على ربع 33 ومقداره 1\4 8. وأصبح العدد الناقص لتكملة 1660 هو 3\4 1 أي واحد وثلاثة أرباع . الواحد يعطينا العدد 1\33، والثلاثة أرباع ما هي إلا 1\2 و1\4، وثلاثة أرباع العدد 1\33 هو 1\44. بذلك أكملنا 1660، ونتيجة القسمة تصبح : 1\44 + 1\33 + 1\4 + 50 .

لوحة قرابين

لوحة ملونة للأميرة نفرتيابت من الدولة القديمة (2565 -2590 قبل الميلاد ) من قبرها بالجيزة وأمامها أعداد لمختلف القرابين . متحف اللوفر، باريس.

مخطوطة رنـــد

في مخطوطة رند Rhind يشرح المصري القديم حساب المساحات وحساب المثلثات .

Il papiro di Rhind.

انظر أيضاً

• أعداد مصرية
• ألواح أخميم الخشبية
• ترجمة حجر رشيد
• بردية موسكو الرياضية
• تحوت إله الكتابة والحساب
• سقد
• كاتب في مصر القديمة

وصلات خارجية

http://books.google.com/books?vid=ISBN0871692325&id=9ToLAAAAIAAJ&dq=PtahHotep&as_brr=1&hl=en Ancient Egyptian Science: A Source Book by Marshall Clagett, 1989]