متعدد حدود لاغرانج
كثير حدود لاغرانج أو متعدد حدود لاغرانج (بالإنجليزية: Lagrange polynomial) في التحليل العددي هو استيفاء كثير الحدود لمجموعة محددة من النقاط بطريقة لاغرانج.[1] اكتشف أولا بواسطة إدوارد ويرينغ في عام 1779 ثم أعيد اكتشافه من قبل ليونهارد أويلر في عام 1783.
بما أنه لايوجد إلا استيفاء واحد لكثير الحدود لمجموعة من النقاط، فمن الخطأ تسمية كثير الحدود باستيفاء لاغرانج لكثير الحدود (Lagrange interpolation polynomial). يجب أن يكون الاسم الأدق هو استيفاء كثير الحدود بطريقة لاغرانج (interpolation polynomial in the Lagrange form).
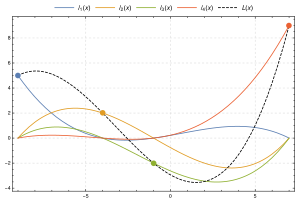
تعريف
ليكن لدينا مجموعة k + 1 من النقاط.
حيث لا تتساوى أي xj لأي نقطتين، فيكون استيفاء كثير الحدود بطريقة لاغرانج هو التركيبة الخطية
لكثيرات حدود لاغرانج الأساسية
ضمان وجود كثيرة الحدود الاستكمالية
نظرية التقريب لفير ستراس لنفرض أن ƒ مغلقة ومتصلة على الفترة [a,b] لكل ε>0، يوجد كثيرة حدود (×)p تحقق الخاصية
[f(x) – p(x) | < ɛ, ∀ x ∈[a,b|
كثيرة حدود لاغرانج الاستكمالية
المشكلة هي في إيجاد كثيرة حدود من الدرجة الأولى تمر في النقطة (x1, y1), (x0 , y0) هو نفس تقريب الدالة f لـ f(x0)= y0 وf(x1) = y1
عن طريقة أو درجة استكمال كثيرة الحدود أو نفس قيم f عند نقاط معينة من نقاط النهاية ويسمى كثيرة حدود إستكمالية.
(L0(x)=(x-x1) / (x0-x1 وَ (L1(x)= (x-x0) / (x1-x0
((p(x) = L0(x) f(x) + L1(x1) f(x1) = ((x-x1) / (x0-x1)) f(x1) + ((x-x0) / (x1-x0
مثال
أوجدي كثيرة الحدود الخطية للاغرانج الاستكمالية المارة في النقطة (4 , 2), (1 , 5) ؟! المطلوب إيجاد كثيرة حدود خطية أي تكون كثيرة الحدود من الدرجة الأولى ويكون إيجادها باستخدام نقطتين وتكون على الصورة
ليكن لدينا وكان المطلوب إيجاد كثير الحدود باستكمال لاغرانج المار من النقطتين . التابع كثير حدود من الدرجة الأولى يعني هو مستقيم يمر بالنقطتين ويمكن استخدام صيغة لاغرانج لإيجاد المعاملات :
تقدير الخطأ في الاستكمال بكثيرات حدود لاغرانج
نظرية (2)
إذا كان لدينا x0,x1,…….,xn أرقام مختلفة في الفترة [a,b] وكانت الدالة [ Cn+1 [a,b ∋ متصلة ولها مشتقات حتى الرتبة n+1 .
ولكل[ x∈[a, b يوجد عدد [ γ(x)∈[a, b يقع بين x0,x1,…….,xn
بحيث يكون
(f(x) – Pn (x) | = ((f(n+1) (γ(x))) / (n+1)!) (x-x0) (x-x1) …. (x-xn|
حيث (Pn(x كثيرة حدود لاغرانج الاستكمالية.
انظر أيضا
مراجع
- ^ Jean-Paul Berrut & Lloyd N. Trefethen (2004). "Barycentric Lagrange Interpolation". SIAM Review. ج. 46 ع. 3: 501–517. DOI:10.1137/S0036144502417715.
| في كومنز صور وملفات عن: متعدد حدود لاغرانج |