قالب:صندوق معلومات دالة رياضية/شرح

اسم
بدل صورة بدل صورة تعليق
تدوين	تدوين
تعريف الدالة	تعريف الدالة
دالة عكسية	دالة عكسية
مشتق الدالة	مشتق دالة
مشتق عكسي (تكامل)	مشتق عكسي
الميزات الأساسية
زوجية أم فردية؟	زوجية أم فردية
مجال الدالة	مجال
المجال المقابل	مجال مقابل
دورة الدالة	دورة الدالة
قيم محددة
القيمة/النهاية عند الصفر	صفر
نهاية الدالة عند +∞	plusinf
نهاية الدالة عند -∞	minusinf
الحدود الأعلى	حد أعلى
الحدود الأدنى	حد أدنى
القيمة/النهاية عند vr1	f1
القيمة/النهاية عند vr2	f2
القيمة/النهاية عند vr3	f3
القيمة/النهاية عند vr4	f4
القيمة/النهاية عند vr5	f5
مواصفات خاصة
خطوط مقاربة	خط مقارب
جذور الدالة	جذر
نقاط حرجة	نقطة حرجة
نقطة انقلاب	inflection
نقاط ثابتة	نقطة ثابتة
ملاحظات	notes

استعمال

{{صندوق معلومات دالة رياضية
| اسم = 
| صورة = <!-- مثل example.jpg -->
| تعليق = 
| حجم صورة = 
| بدل صورة = 
| تدوين =
| تعريف الدالة =
| دالة عكسية =
| مشتق دالة =
| مشتق عكسي =
| زوجية أم فردية = 
| مجال = 
| مجال مقابل = 
| دورة الدالة = 
| plusinf = 
| minusinf = 
| صفر = 
| حد أعلى = 
| حد أدنى = 
| vr1 = 
| f1 = 
| vr2 = 
| f2 = 
| vr3 = 
| f3 = 
| vr4 = 
| f4 = 
| vr5 = 
| f5 = 
| خط مقارب = 
| جذر = 
| نقطة حرجة = 
| نقطة انقلاب = 
| نقطة ثابتة = 
| ملاحظات = 
}}

مثال

مثال على ذلك صندوق معلومات لدالة "مربع عدد".

دالة "مربع عدد"
الرسم البياني لدالة مربع عدد له شكل قطع مكافئ. الرسم البياني لدالة مربع عدد له شكل قطع مكافئ.
تدوين	$x^2$
دالة عكسية	$\sqrt{x}$
مشتق الدالة	$2x$
مشتق عكسي (تكامل)	$\frac{x^3}{3}$
الميزات الأساسية
زوجية أم فردية؟	زوجية
مجال الدالة	$]-\mathrm{\infty },+\mathrm{\infty }[$
المجال المقابل	$[0,+\mathrm{\infty }[$
قيم محددة
القيمة/النهاية عند الصفر	0
نهاية الدالة عند +∞	$+\mathrm{\infty }$
نهاية الدالة عند -∞	$+\mathrm{\infty }$
الحدود الأدنى	0
القيمة/النهاية عند 1	1
القيمة/النهاية عند 2	4
القيمة/النهاية عند -1	1
القيمة/النهاية عند -2	4
جذور الدالة	0
نقاط حرجة	0
نقاط ثابتة	1 و0

{{صندوق معلومات دالة رياضية
| اسم = الدالة "مربع عدد"
| صورة = ملف:Parabola2.svg
| تعليق = الرسم البياني لدالة مربع عدد له شكل [[قطع مكافئ]].
| حجم صورة = 
| بدل صورة = 
| تدوين = <math>x^2</math>
| دالة عكسية = <math>\sqrt{x}</math>
| مشتق دالة = <math>2x</math>
| مشتق عكسي = <math>\frac{x^3}{3}</math>
| زوجية أم فردية = زوجية
| مجال = <math>]-\infty , +\infty[</math>
| مجال مقابل = <math>[0 , + \infty[</math>
| دالة دورية = 
|plusinf = 
<math>+\infty</math>
| minusinf =
<math>+\infty</math>
| صفر = 0
| حد أعلى = 
| حد أدنى = 0
| vr1 = 
1
| f1 = 
1
| vr2 = 
2
| f2 =
4 
| vr3 = {{يسار إلى يمين|-1}} 
| f3 =
1
| vr4 = {{يسار إلى يمين|-2}}
| f4 =
4
| vr5 = 
| f5 = 
| خط مقارب = 
| جذر = 0
| نقطة حرجة = 0
| نقطة ثابتة = 1 و0
| ملاحظات = 
}}

مثال آخر على ذلك هو ص.م لدالة اللوغاريتم الطبيعي.

لوغاريتم طبيعي
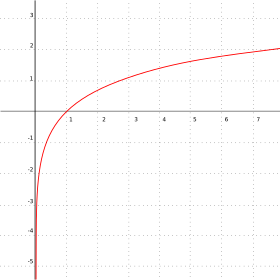منحنى دالة اللوغاريتم الطبيعي. تتزايد الدالة ببطء إلى زائد ما لا نهاية له عندما يصير x كبيرا، بينما تذهب إلى ناقص ما لا نهاية له بسرعة كبيرة عندما يقترب x من الصفر. محور y هو خط مقارب للدالة. منحنى دالة اللوغاريتم الطبيعي. تتزايد الدالة ببطء إلى زائد ما لا نهاية له عندما يصير x كبيرا، بينما تذهب إلى ناقص ما لا نهاية له بسرعة كبيرة عندما يقترب x من الصفر. محور y هو خط مقارب للدالة.
تدوين	$\ln (x)$
تعريف الدالة	$\ln (x)=\underset{1}{\overset{x}{\int }}\frac{dt}{t}$
دالة عكسية	$e^x$
مشتق الدالة	$\frac{1}{x}$ على المجال $]0;+\mathrm{\infty }[$
مشتق عكسي (تكامل)	$x\ln (x)-x+C$
الميزات الأساسية
مجال الدالة	${\mathbb{ℝ}}_{+}^{*}=]0;+\mathrm{\infty }[$
المجال المقابل	$\mathbb{ℝ}$
قيم محددة
القيمة/النهاية عند الصفر	على اليمين: $-\mathrm{\infty }$
نهاية الدالة عند +∞	$+\mathrm{\infty }$
القيمة/النهاية عند 1	0
القيمة/النهاية عند e	1
خطوط مقاربة	$x=0$
جذور الدالة	1

{{صندوق معلومات دالة رياضية
| اسم = لوغاريتم طبيعي
| صورة = Graph of ln x.svg
| تعليق = منحنى دالة اللوغاريتم الطبيعي. تتزايد الدالة ببطء إلى زائد ما لا نهاية له عندما يصير x كبيرا، بينما تذهب إلى ناقص ما لا نهاية له بسرعة كبيرة عندما يقترب x من الصفر. محور y هو [[خط مقارب]] للدالة.
| حجم صورة = 
| بدل صورة = 
| زوجية أم فردية = 
| تدوين = <math>\ln (x)</math>
| تعريف الدالة = <math>\ln (x) =\int_1^x \frac{dt}{t}</math>
| دالة عكسية = <math>e^x</math>
| مشتق دالة = <math>\frac{1}{x}</math> على المجال <math>]0 ; + \infty[</math>
| مشتق عكسي = <math>x\ln (x) - x + C</math>
| مجال = <math>\R_+^* = ]0 ; + \infty[</math>
| مجال مقابل = <math>\R</math>
| دالة دورية = 
| plusinf =
<math>+\infty</math>
| minusinf = 
| vr1 = 1
| صفر = على اليمين:
<math>-\infty</math>
| حد أعلى = 
| حد أدنى = 
| f1 = 0
| vr2 = [[ه (رياضيات)|e]]
| f2 = 1
| vr3 = 
| f3 = 
| vr4 = 
| f4 = 
| vr5 = 
| f5 = 
| خط مقارب = <math>x=0</math>
| جذر = 1 
| ملاحظات = 
}}