|
تضامنًا مع حق الشعب الفلسطيني |
مبرهنة براهماغوبتا
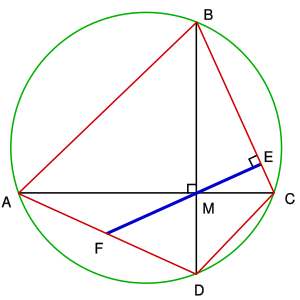
مبرهنة براهماغوبتا (بالإنجليزية: Brahmagupta's theorem) في الهندسة الرياضية تنص على أنه إذا كان لرباعي دائري أقطار متعامدة، فإن العمود المنشأ من نقطة تقاطع أقطار المضلع على أحد أضلاعه ينصف الضلع المقابل.[1] سميت هذه المبرهنة على اسم عالم الرياضيات الهندي براهماغوبتا.
البرهان

يتعين علينا إثبات أن AF = FD. سوف نبرهن أن AF وFD هما في الحقيقة مساويان لـ FM.
لإثبات أن AF = FM، أولاً لاحظ أن الزاويتين FAM وCBM هما متساويتان، لأنهما زاويتان محيطيتان تشتركان في نفس قوس الدائرة. لاحظ أيضاً، الزاويتان CBM وCME كل منهما متممة للزاوية BCM (أي أن كل منهما يضاف للزاوية ليكون °90)، وهما لذلك متساويتان. أخيراً، الزاويتان CME وFMA نفسهما. بالتالي، AFM هو مثلث متساوي الساقين، وعليه فإن الضلعين AF وFM متساويان.
بالمثل يمكن إثبات أن FD = FM: الزوايا FDM، BCM، BME وDMF هي جميعا متساوية، بالتالي DFM مثلث متساوي الساقين، إذن FD = FM. ينتج من ذلك أن AF = FD، كما تنص النظرية.
مراجع
- ^ "معلومات عن مبرهنة براهماغوبتا على موقع mathworld.wolfram.com". mathworld.wolfram.com. مؤرشف من الأصل في 2019-05-28.
وصلات خارجية
| مبرهنة براهماغوبتا في المشاريع الشقيقة: | |