تقييد مدي
الانغلاق المداري أو التقييد المدِّي (بالإنجليزية: Tidal Locking) هو ظاهرة بقاء جرم سماوي مواجهاً لجسم آخر أثناء دورته حوله كما هو الحال مع القمر حين يواجه الأرض بوجه واحد طوال الوقت تقريباً. يحدث هذا التقييد بسبب اختلاف التدرج الثقالي أو قوى المد والجزر وذلك بجعل أحد جانبي الجرم السماوي مرغماً على البقاء في مواجهة الجسم الآخر. غالباً ما تحدث هذه الظاهرة مع الأقمار فقط طيلة دورانها حول أجسام أكبر منها كتلة. عملياً يفاد من هذه الظاهرة في تقييد الأقمار الصناعية بمواجهة الأرض أو الكواكب التي تدور حولها.
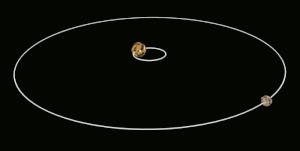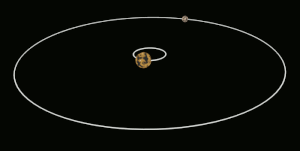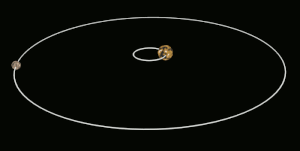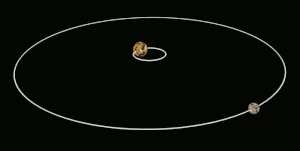

في علم الفلك تعرف الحركة التزامنية بأنه مصطلح للأجرام التي تدور حول جرم آخر في مدار معين بحيث يكون الزمن اللازم لاتمام دورة حول محوره أكبر من الزمن اللازم لاتمام دورة مدارية واحدة. لذلك يبقى نصفه فقط مواجه الجرم الذي يدور حوله بشكل دائم.
ومثال على ذلك القمر ذو حركة تزامنية [1] في دورانه حول الأرض. وفي الواقع معظم أقمار النظام الشمسي ذوات حركة تزأمنية مع كواكبها.
تفسير الظاهرة
في الميكانيكا الكلاسيكية يمكن تفسير ذلك بأنه يعود لتغير قيمة القوة لوحدة الكتل التي يؤثر بها جسم بجاذبيته الأكبر على جسم آخر عبر امتداد القطر.
لو أن لدينا جسمين A و B بحيث A أكبر من B فإن معدل التغير في الدوران اللازم لقفل الجسم B إلى الجسم A ينشأ بسبب عزم قوة الجاذبية لـA المؤثرة على على نتوءات مختلفة في B (تذكر أن الأجسام كروية غالبا وليست نقطية) وهذا بدوره يشوه الاتزان الثقالي بشكل طفيف بحيث يبدو ممتداً في محور B المواجه والممتد نحو A بعكس محور B العمودي على المسافة بين B و A، وتعرف هذه التشويهات المؤقتة بالنتوءات المدّية.
عند عدم الاستقرار بتقيد B إلى A فإن هذه النتوءات على سطح B تحاول دائما التخلف والانجذاب نحو الجهة المقابلة لـA في الوقت الذي يحاول الجسم B إعادة تشكيل نفسه كما كان متماثلا بفضل قوى جاذبيته. يستمر الأمر على هذا المنوال ويفقد الجسم B جزءاُ من زخم الحركة الدورانية والطاقة الحركية في سبيل التغلب على هذه القوى المدّية حتى يأتي زمن يكون فيه الجسم قد فقد كل زخم الحركة الدورانية ولا يتبقى منها سوى زخم الحركة الدورانية المقيدة.
نظراً لقانون بقاء الزخم الزاوي في المنظومة A-b ككل فإن الجزء المفقود من الزخم الدوراني في B يتحول إلى جزئين أحدهم يؤثر بشكل طفيف في دوران A والآخر يظهر بشكل ملحوظ في اتساع المدار لـB حول A.
قياس زمني
أحد التقديرات لحساب الفترة الزمنية اللازمة لحدوث عملية التقييد ممكنة من العلاقة التالية:[2]
حيث
- معدل الدوران المغزلي الابتدائي بوحدات راديان في الثانية.
- is the نصف المحور الرئيسي لحركة القمر حول الكوكب.
- عزم عطالة القمر.
- دالة التبدد للقمر.
- ثابت الجذب العام
- كتلة الكوكب
- كتلة القمر
- رقم لوف للقمر
- نصف قطر القمر.
Q و لا تتوافر معلومات كافية عنهما عدا لقمر الأرض حيث . مع ذلك يمك تقدير Q≈100 و
حيث
- كثافة القمر
- جاذبية سطح القمر
- صلابة القمر وتقدر بـ 3×1010 Nm−2 للأجسام الصخرية و 4×109 Nm−2 للجليدية.
نظراً لكبر الاستبعادية، يمكن تبسيط العلاة السابقة أكثر، بافتراض , Q = 100, ومن المنطقي تخمين دورتين كل يوم في حالة عدم التقييد الابتدائية.
حيث الكتل بالكيلوغرام، المسافات بالأمتار، وμ in Nm−2. μ يمكن تقديرها في أسوأ الأحوال بـ 3×1010 Nm−2 للكتل الصخرية و 4×109 Nm−2 للكتل الجليدية.
أقمار
كواكب
انظر أيضاً
المصادر
- ^ synodic period | astronomy | Britannica.com نسخة محفوظة 27 أبريل 2020 على موقع واي باك مشين.
- ^ B. Gladman؛ وآخرون (1996). "Synchronous Locking of Tidally Evolving Satellites". Icarus. ج. 122: 166. DOI:10.1006/icar.1996.0117.
{{استشهاد بدورية محكمة}}: Explicit use of et al. in:|مؤلف=(مساعدة) (See pages 169-170 of this article. Formula (9) is quoted here, which comes from S.J. Peale, Rotation histories of the natural satellites, in J.A. Burns، المحرر (1977). Planetary Satellites. Tucson: University of Arizona Press. ص. 87–112.)