آلة آتوود

اخترع القس جورج آتوود آلة آتوود (أو جهاز آتوود) في عام 1784 كتجربةٍ معملية من أجل إثبات قوانين الحركة الميكانيكية من خلال التسارع الثابت. وتُعد آلة أتوود وسيلةً تعليميةً شائعة في الفصول الدراسية وتُستخدم لشرح مبادئ الميكانيكا الكلاسيكية.

تتكون آلة آتوود المثالية من كتلتين m₁ وm₂، متصلتين بحبل غير قابل للمد وعديم الكتلة يلف حول بكرة مثالية عديمة الكتلة. ^[1]

عندما تكون m₁ = m₂، تكون الآلة في حالة توازن محايد بغض النظر عن وضع الأوزان.

عندما تكون m₁ ≠ m₂؛ يحدث تسارع منتظم لكلتا الكتلتين.

معادلة التسارع الثابت

مخططات الجسم الحر للكتلتين المعلقتين في آلة آتوود. وتفيد مصطلحات الإشارات لدينا، كما تشير متجهات التسارع، أن m₁ تتسارع نزولاً وأن m₂ تتسارع صعودًا، كما هو الحال إذا كانت m₁ > m₂

يمكننا استنتاج معادلة للتسارع من خلال استخدام تحليل القوى. فإذا نظرنا إلى حبل عديم الكتلة وغير قابل للمد وبكرة مثالية عديمة الكتلة، فستكون القوى التي يجب أخذها في الاعتبار فقط هي: قوة الشد (T)، ووزن الكتلتين (W₁ وW₂). لإيجاد التسارع، يجب الأخذ في الاعتبار القوى المؤثرة على كل كتلة مفردة. ومن خلال استخدام قانون نيوتن الثاني (حيث تفيد مصطلحات الإشارات أن $m_{1} > m_{2}$ )، يمكننا استنباط نظام معادلات للتسارع (a).

كاصطلاح للإشارة، نفترض أن a تكون موجبة عندما تتسارع نزولاً لـ $m_{1}$ , وأن a تكون موجبة عندما تتسارع صعودًا لـ $m_{2}$ .. ومن ثم يكون وزن $m_{1}$ و $m_{2}$ هو ببساطة $W_{1} = m_{1} g$ و $W_{2} = m_{2} g$ على التوالي.

القوى المؤثرة على m₁:

$m_{1} g - T = m_{1} a$

والقوى المؤثرة على m₂:

$T - m_{2} g = m_{2} a$

وبجمع المعادلتين السابقتين، نحصل على

$m_{1} g - m_{2} g = m_{1} a + m_{2} a$ ,

وتصبح الصيغة النهائية للتسارع لدينا

$a = g \frac{m_{1} - m_{2}}{m_{1} + m_{2}}$

وبالعكس، يمكن إيجاد التسارع الناجم عن الجاذبية،g، عن طريق ضبط توقيت حركة الأوزان وحساب قيمة التسارع المنتظم a: $d = \frac{1}{2} a t^{2}$ .

تُستخدم آلة آتوود أحيانًا لشرح طريقة لاغرانج لاستنباط معادلات الحركة.

معادلة الشد

قد يكون من المفيد معرفة معادلة شد الوتر. لتقدير الشد، يتم تعويض المعادلة بالتسارع في أيٍ من معادلتيّ القوى.

$a = g \frac{m_{1} - m_{2}}{m_{1} + m_{2}}$

على سبيل المثال، عند التعويض بـ $m_{1} a = m_{1} g - T$ ، نحصل على

$T = \frac{2 g m_{1} m_{2}}{m_{1} + m_{2}}$

يمكن إيجاد الشد عن طريق استخدام هذه الطريقة.

معادلات لبكرة بها قصور واحتكاك

بالنسبة للاختلافات الصغيرة جدًا بين كتل m₁ وm₂، لا يمكن تجاهل العطالة الدورانية I لبكرة نصف قطرها r. ويتم الحصول على التسارع الزاويّ للبكرة من خلال وضع عدم الانزلاق:

$α = \frac{a}{r},$

حيث تكون $α$ هي التسارع الزاويّ. فبالتالي يكون عزم الدوران هو:

$τ_{n e t} = (T_{1} - T_{2}) r - τ_{f r i c t i o n} = I α$

بضم قانون نيوتن الثاني للكتل المعلقة، وحل T₁ وT₂، وa، نحصل على:

التسارع:

a = \frac{g (m_{1} - m_{2}) - \frac{τ_{f r i c t i o n}}{r}}{m_{1} + m_{2} + \frac{I}{r^{2}}}

الشد في أقرب جزء من الوتر لـm₁:

T_{1} = \frac{m_{1} g (2 m_{2} + \frac{I}{r^{2}} + \frac{a u_{f r i c t i o n}}{r g})}{m_{1} + m_{2} + \frac{I}{r^{2}}}

الشد في أقرب جزء من الوتر لـm₂:

T_{2} = \frac{m_{2} g (2 m_{1} + \frac{I}{r^{2}} + \frac{a u_{f r i c t i o n}}{r g})}{m_{1} + m_{2} + \frac{I}{r^{2}}}

في حال تجاهل الاحتكاك (وليس قصور البكرة ولا قوة سحب الوتر على حافة البكرة)، يمكن تبسيط تلك المعادلات في صورة النتائج التالية:

التسارع:

a = \frac{g (m_{1} - m_{2})}{m_{1} + m_{2} + \frac{I}{r^{2}}}

الشد في أقرب جزء من الوتر لـm₁:

T_{1} = \frac{m_{1} g (2 m_{2} + \frac{I}{r^{2}})}{m_{1} + m_{2} + \frac{I}{r^{2}}}

الشد في أقرب جزء من الوتر لـm₂:

T_{2} = \frac{m_{2} g (2 m_{1} + \frac{I}{r^{2}})}{m_{1} + m_{2} + \frac{I}{r^{2}}}

تطبيقات عملية

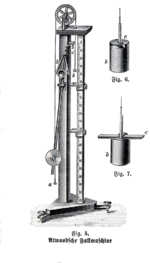
تشير رسوم آتوود الإيضاحية الأصلية إلى استناد محور العجلة الرئيسي على حواف أربع عجلات أخرى، لتقليل قوى الاحتكاك الناتجة عن المحامل. وتتبع العديد من التطبيقات التاريخية القديمة هذا التصميم.

تقارب فكرة المصعد الذي يضم ثقل موازن فكرة آلة آتوود المثالية، حيث يتم من خلالها تخفيف ثقل حمل مقصورة المصعد عن محرك القيادة - ويكون عليه فقط التغلب على فرق الوزن وقصور كلتا الكتلتين. ويتم تطبيق الفكرة ذاتها على سكك حديد القطار الجبلي المائل الذي يتكون من عربتين متصلتين على مسارات مائلة.

انظر أيضًا

بندول كاتر
آلة آتوود الدوارة
Professor Greenslade's account on the Atwood Machine

ملاحظات

^ Tipler، Paul A. (1991). Physics For Scientists and Engineers, Third Edition, Extended Version. New York: Worth Publishers. Chapter 6, example 6-13, page 160.

"Atwood's Machine" by Enrique Zeleny, The Wolfram Demonstrations Project.

في كومنز صور وملفات عن: آلة آتوود

[1] Tipler، Paul A. (1991). Physics For Scientists and Engineers, Third Edition, Extended Version. New York: Worth Publishers. Chapter 6, example 6-13, page 160.

[1]