|
تضامنًا مع حق الشعب الفلسطيني |
سلسلة شتاينر
سلسلة شتاينر(Steiner chain)، في الهندسة، هي سلسلة من الدوائر المتماسة لدائرتين معلومتين وغير متقاطعتين. كل دائرة من السلسلة تكون أيضا متماسة للدائرة السابقة والتالية لها. تكون سلسلة شتاينر مغلقة عندما تكون الدائرتين الأولى والأخيرة متماسة لبعضهما البعض. يجب البدء بدائرتين غير متقاطعتين لبناء السلسلة. وهذا يعني ان الدائرة الأصغر يمكن ان تكون داخلية أو خارجية بالنسبة للدائرة الأكبر. في هذه الحالتين، تقع مراكز الدوائر المكونة للسلسلة على قطع ناقص أو قطع الزائد، على التوالي.
تمت تسمية سلسلة شتاينر نسبة للعالم السويسري ياكوب شتاينر، الذي عرفها في القرن التاسع عشر واكتشف العديد من خصائصها. كما يُنسب إليه الفضل في صياغة مسامية شتاينر.[1] تنص على أنه إذا كانت هناك سلسلة مغلقة واحدة على الأقل من الدوائر المتماسة لدائرتين معلومتين، فإن هناك عدد لا حصر له من الدوائر الأخرى.[2]
اجراءات هندسية
معلوم دائرتين (اللون الأحمر) متحدة المستوى، وبدون نقاط مشتركة بينهما، من الممكن دائما تحويلهما، عن طريق الانعكاس، إلى دائرتين متحدتي المركز.
الانشاءات الهندسية:
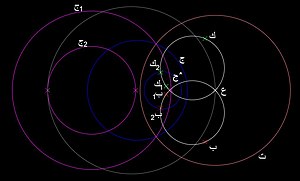
- نأخذ في الاعتبار أي دائرتين ج وج^ (الشكل 3)؛ بلا نقاط مشتركة، والتي تحددان حزمة من الدوائر؛
- نعين نقطة ب بحيث لا تنتمي إلى أي واحدة من الدائرتين
- نفترض أن ب1 و ب2 هما انعكاس ب بالنسبة للدائرتين ج وج^
- نرسم الدائرة س1 التي تمر بالنقاط ب، ب1 و ب2
- وبطريقة مماثلة نرسم الدائرة س2 ، بحيث تمر بالنقاط ك، ك1 و ك2
- نرسم دائرة ت بحيث يقع مركزها في نقطة التقاطع ع، بين الدائرتين س1 و س2
- نحدد انعكاس الدائرتين ج، ج^ بالنسبة للدائرة ت وهكذا نحصل على دائرتين متحدتي المركز
معرض
-
انشاءات هندسية وصفية لرسم سلسلة شتاينر
-
اجراء هندسي وصفي لتحديد سلسلة شتاينر
-
سلسلة شتاينر ولكن بمخروطيات غير متشابهة
-
سلسلة شتاينر ولكن لأسطح إهليلجيه عامة (متقابلة اثنين اثنين لبعضها البعض)
-
إنشاءات هندسية وصفية لعملية تعاكس ( inversion) دائرة زرقاء بالنسبة لدائرة أخرى صفراء ، حيث الزرقاء لا تمر بمركز الصفراء
-
إجراء وصفي لتحديد سلسلة شتاينر باستخدام التعاكس
مراجع
- ^ تعريف البورمية في مفردات الموسوعة تريكاني (Treccani) نسخة محفوظة 24 فبراير 2020 على موقع واي باك مشين.
- ^ (EN) H.S.M. Coxeter, S.L. Greitzer, Geometry Revisited (PDF), in New Mathematical Library, vol. 19, The Mathematical Association of America, 1967, 124-125
| سلسلة شتاينر في المشاريع الشقيقة: | |





