|
تضامنًا مع حق الشعب الفلسطيني |
طور موجة
طور موجة أو طور حركة اهتزازية، (بالإنجليزية: phase) خاصية تعبرعن توافق أو عدم توافق موجات ذات طول موجىّ واحد (وبالتالى تردد واحد).[1][2][3]

حيث تحدد الإزاحة الابتدائية للموجه عن الزمن t = 0. ويمكن اعتبار طور الموجة مثالا للحركة التوافقية البسيطة. فالموجه يمكن وصفها ب طول الموجة المطال وطور الموجه. إي إذا أردنا حساب موقع رقاص ساعة عند لحظة معينة نحتاج لمعرفة تلك الثلاثة خواص للرقاص بالإضافة إلى الزمن. وينطبق نفس النظام على الحركة الموجية الجيبية عند نقطة ما في المكان ولمدة فترة زمنية، أو عبر مسافة معينة وعند نقطة معينة من الزمن. والحركة التوافقية البسيطة ما هي إلا إزاحة تتغير دوريا كما يوضحها الشكل.
ويمكن وصف تغير الإزاحة x مع الزمن (t) بالعلاقة:
حيث: A المطال وهو النهاية العظمى للإزاحة،
T زمن الدورة
ƒ التردد.
- هي طور الموجة والتي تحدد الإزاحة الابتدائية عند الزمن t = 0.
والحركة بالتردد ƒ يقترن بزمن دورة الموجة
ويلفت نظرنا أن رغم اختلاف دالة الإزاحة الابتدائية عن الدالة الجيبية الموصوفة أعلاه إلا أنهما يتميزان بنفس الطور.
الدورة
تعرف الدورة T بأنها زمن دورة واحدة (أنظر الشكل)، أو زمن طول الموجة، الزمن بين قمتين متتاليتين لموجة أو الزمن بين قاعين متتاليين للموجة.
بالمثل: نأخد مثال الأرض في دورانها حول الشمس. تدور الأرض في فلكها بطريقة دورية حول الشمس، من الصيف إلى الخريف إلى الشتاء إلى الربيع، ثم يأتي الصيف مرة ثانية، وهكذا فتكون دورة الأرض هي 365 يوم أو سنة.
كذلك تدور الأرض حول محورها خلال 24 ساعة، أي أن زمن دورة الأرض حول نفسها 24 =T ساعة.
دورة التيار الكهربائي المتردد: تتغير شدة التيار الكهربائي المتردد بطريقة موجية، حيث يهبط من قمة عظمى إلى قاع ثم يعلو ثانيا ليصل إلى قمة عظمى ثانية (قارن الشكل اعلاه). الزمن بين قمتين متتاليتين للتيار المتردد هو زمن الدورة.
رأينا أعلاه العلاقة بين زمن الدورة T والتردد ƒ:
يتضح من ذلك أن معادلة جبرية واحدة وهي معادل موجة، مثل يمكن بواسطتها وصف تغير التيار المتردد ووصف تغير الجهد المتردد، كما يمكن بها وصف حركة دوران الأرض حول محورها، وحركة دوران الأرض حول الشمس. في نفس الوقت يمكن للمعادلة الموجية وصف حركة رقاص الساعة.
ولعل القاريء قد توصل إلى أن دورة رقاص الساعة هي 1 ثانية.
اختلاف طور موجتين لهما نفس التردد
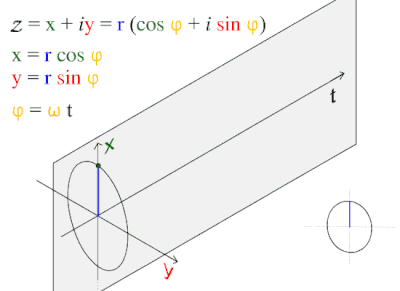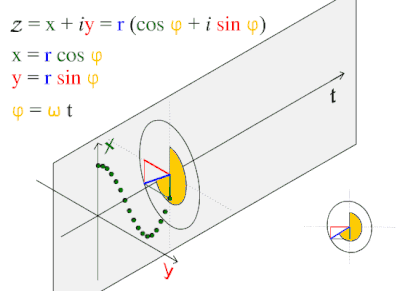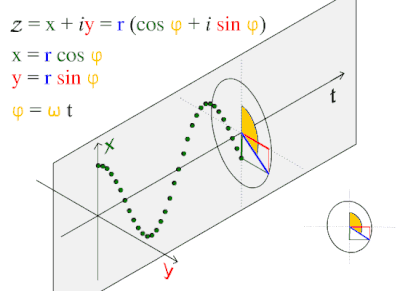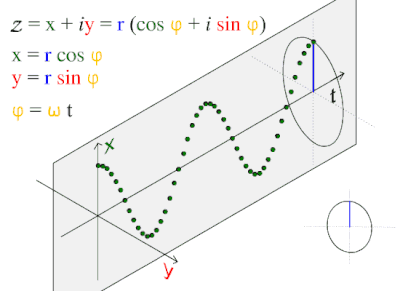
نعتبر حركة موجة جيبية طبقا للمعادلة:
وأردنا تطبيقها في حالة التيار المتردد نحصل على الآتي:
حيث: التردد ƒ هرتز
- وزمن الدورة T ثانية.
- زاوية الطور
- زاوية الطور الصفرية هي زاوية الطور عند الزمن.
- فرق الطور هو الفرق بين طوري موجتين لهما نفس التردد (بالتالي نفس طول الموجة).
فرق الطور
لنأخذ مثال الجهد المتردد، ومعادلته كالآتي:
حيث:
- هو القيمة العظمى للجهد الكهربائي (ويسمى مطال الجهد)
ونقارن دالة الجهد بدالة التيار:
ونحسب فرق الطور كالآتي:
- أو ( ).
انزياح الطور

يوضح الشكل انزياح الطور بين موجتين لهما نفس التردد. ويقدر انزياح الطور بالزاوية .
وبالنسبة إلى موجة جيبية طويلة لا نهائية يكون التغير في الزاوية مساويا للإزاحة الزمنية بين الموجتين.
فإذا كانت الفرق الزمنيللدورة،
تصبح:
=
ويصبح «طورها»
قد انزاح بمقدار:
اتساق الطور



يعبر اتساق الموجات في الفيزياء عن صلاحية موجة لكونها في مرحلة معينة من الطور متوافقة مع أطوار موجات أخرى، تلك الموجات الأخرى تكون عادة لها نفس طول الموجة. يعمل جهاز الليزر على اتساق موجات الضوء الصادر منه عن طريق عكس الضوء داخله عدة مرات. وباتساق الموجات يكون شعاع الليزر شديدا ورفيعا وله طول موجة واحد. يستخدم اتساق الموجات في أجهزة عديدة مثل مقياس ميكلسون للتداخل كما هناك تجربة شهيرة لميكلسون استخدمها في البحث عن «أثير الضوء» وبين بها أنه لا يوجد شيء اسمه الأثير، تلك هي تجربة ميكلسون ومورلي.
وفي الفيزياء تصف ميكانيكا الكم الجسيمات على أنها موجات . وهي تستخدم أنواعا من الدوال الموجية المركبة، ونظرا لأن مربع مطال الموجة يتناسب مع احتمال وجود الجسيم عند نقطة معينة، فتكون الدالة الموجية مرتبطة بالطور. وتتيح رياضة الأعداد المركبة لوصف التداخل بين الموجات التي تعبر عنها ميكانيكا الكم . ولذلك يتحكم طور الجسيم في خصائصه الكمومية.
اقرأ أيضا
- تيار أحادي الطور
- نظام متعدد الأطوار
- ثلاثي الأطوار
- زاوية الطور
- تغير الطور
- طول الموجة
- تشويه الطور
- تردد فراغي
- العدد الموجي
- قانون براج
- حيود براج
- تذبذب
- تداخل الموجات
- تداخل الإشارات
- مرشح التداخل
- جهاز تداخل صفري
- قياس التداخل
- قياس التداخل ثنائي الاستقطاب
مراجع
- ^ "Time and Frequency from A to Z". "Phase". المعهد الوطني للمعايير والتقنية (NIST). مؤرشف من الأصل في 2016-08-16. اطلع عليه بتاريخ 2016-06-12.
- ^ Clint Goss؛ Barry Higgins (2013). "The Warble". Flutopedia. مؤرشف من الأصل في 2017-12-16. اطلع عليه بتاريخ 2013-03-06.
- ^ Ballou، Glen (2005). Handbook for sound engineers (ط. 3). Focal Press, Gulf Professional Publishing. ص. 1499. ISBN:0-240-80758-8. مؤرشف من الأصل في 2017-03-14.
| في كومنز صور وملفات عن: طور موجة |