حلزون لوغاريتمي
(بالتحويل من اللولب اللوغاريتمي)
الحلزون اللوغاريتمي (بالإنجليزية: Logarithmic spiral) هو منحنى حلزوني ذو تشابه ذاتي والذي يظهر غالبًا في الطبيعة. تم وصف الحلزون اللوغاريتمي لأول مرة بواسطة رينيه ديكارت ثم قام ياكوب برنولي بالتحقيق فيه على نطاق واسع.
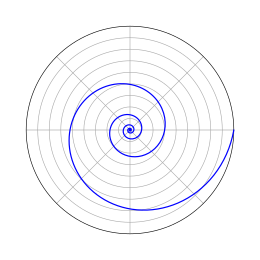
في النظام الإحداثي القطبي يمكن رسم الحلزون اللوغاريتمي وفق الآتي:[1]
أو
مع كون قاعدة اللوغاريتمات الطبيعية وكونها ثوابت حقيقية في الشكل البارامتري، يكون المنحنى:
مع العددين الحقيقين و. يحتوي الحلزون على خاصية أن الزاوية بين المماس والقطر عند النقطة ثابت. يمكن التعبير عن هذه الخاصية في علاقات هندسية تفاضلية
مشتق ال يتناسب مع المعلمة بمعنى آخر () يصبح الحلزون دائرة من نصف القطر وفي الحد الذي يقترب من اللانهاية يميل الحلزون نحو نصف مستقيم، زاوية ال تسمى pitch
معرض صور
المراجع
- ^ Priya Hemenway (2005). Divine Proportion: Φ Phi in Art, Nature, and Science. Sterling Publishing Co. ISBN:1-4027-3522-7. مؤرشف من الأصل في 2022-06-22.
وصلات خارجية
- Spira mirabilis history and math
- Nemiroff، R.؛ Bonnell، J.، المحررون (25 سبتمبر 2003). "Hurricane Isabel vs. the Whirlpool Galaxy". صورة اليوم الفلكية. ناسا.
- Nemiroff، R.؛ Bonnell، J.، المحررون (17 مايو 2008). "Typhoon Rammasun vs. the Pinwheel Galaxy". صورة اليوم الفلكية. ناسا.
- SpiralZoom.com, an educational website about the science of pattern formation, spirals in nature, and spirals in the mythic imagination.
- Online exploration using JSXGraph (JavaScript)
| في كومنز صور وملفات عن: حلزون لوغاريتمي |