|
تضامنًا مع حق الشعب الفلسطيني |
متسلسلة تايلور

| جزء من سلسلة مقالات حول |
| التفاضل والتكامل |
|---|
| بوابة رياضيات |
مُتَسَلْسِلَةُ تَايْلُور[عر 1][عر 2] أو سِلْسِلَةُ تَايْلُور[عر 3] (بالإنجليزية: Taylor series) أو مَفْكُوكُ تَايْلُور[عر 4] أو نَشْرُ تَايْلُور[عر 5] (بالإنجليزية: Taylor expansion) لدالة ما هي مجموع غير منتهٍ من الحدود التي يُعبَّر عنها بدلالة مشتقات الدالة في نقطة محددة. تكون معظم الدوال الشائعة ومجموع متسلسلة تايلور الخاصة بها متساويتين بالقرب من هذه النقطة. سميت سلسلة تايلور على اسم العالم الإنجليزي بروك تايلور، الذي أدخلها في عام 1715. وتسمى متسلسلة تايلور أيضًا متسلسلة ماكلورين عندما تكون المشتقات عند النقطة 0، تيمنًا بالعالم الإسكتلندي كولين ماكلورين، الذي استخدم هذه الحالة الخاصة من متسلسلة تايلور على نطاق واسع في منتصف القرن الثامن عشر.
المجموع الجزئي المكون من حدود n + 1 الأولى لمتسلسلة تايلور هو كثير الحدود من الدرجة n يسمى كثير حدود تايلور للدالة من الدرجة n. تعد معادلات تايلور كثيرة الحدود تقديرات تقريبية لدالة ما، والتي تصبح أكثر دقة عمومًا عندما تتزايد n. تعطي مبرهنة تايلور تقديرات كمية للخطأ الناتج عن استخدام مثل هذه التقديرات التقريبية. إذا كانت متسلسلة تايلور للدالة متقاربة، فإن مجموعها هي نهاية المتتالية اللانهائية لكثير الحدود لتايلور. قد تختلف الدالة عن مجموع متسلسلة تايلور الخاصة بها، حتى لو كانت متسلسلة تايلور متقاربة. تكون الدالة تحليلية عند نقطة x إذا كانت مساوية لمجموع متسلسلة تايلور الخاصة بها في فترة مفتوحة (أو قرص مفتوح في المستوي المركب) تحوي x. هذا يعني أن الدالة تحليلية في كل نقطة من الفترة (أو القرص).
التعريف
متسلسلة تايلور لدالة حقيقية أو ذات قيم مركبة f(x) من الصنف C∞ (أي قابلة للتفاضل لانهائيًّا) عند عدد حقيقي أو مركب a هي متسلسلة القوى:[1]
وفيها n! ترمز إلى عاملي n. يمكن كتابة المتسلسلة السابقة بتدوين سيغما الأكثر اختصارًا كما يأتي:
وفي هذا الشكل تشير f(n)(a) إلى مشتق f من الدرجة n عند النقطة a (المشتقة من الدرجة 0 للدالة f معرفة على أنها f نفسها و(x − a)0 و 0! معرفتان على أنها 1.)
عندما يكون a = 0، تأخذ متسلسلة ماكلورين الشكل التالي:[1]
بتدوين سيغما الأكثر اختصارًا:
الأمثلة
متسلسلة تايلور لأي كثير حدود هو كثير الحدود نفسه.
متسلسلة ماكلورين لـ 11 − x هي المتسلسلة الهندسية التالية:
إذن، بتعويض x بـ 1 − x، متسلسلة تايلور لـ 1x عند a = 1 هي:
بمكاملة متسلسلة ماكلورين أعلاه، تنتج متسلسلة ماكلورين: ln(1 − x), وفيها يشير ln إلى اللوغاريتم الطبيعي:
متسلسلة تايلور الموافقة للدالة ln x عند a = 1 هي:
متسلسلة تايلور الموافقة للدالة ln x عند أي نقطة a لا تساوي الصفر هي:
متسلسلة ماكلورين للدالة الأسية ex هي:
المفكوك أعلاه مستمر لأن مشتق ex بالنسبة لـ x هو نفسه ex، وe0 تساوي 1. يجعل هذا الحدود (x − 0)n في البسط وn! في المقام لأي حد في المتسلسلة اللانهائية.
التاريخ
نظر الفيلسوف الإغريقي زينون الإيلي في مسألة جمع متسلسلة لانهائية لتحقيق نتيجة منتهية، لكنهُ رفضها لأنها مستحيلة؛[2] وكانت النتيجة مفارقة زينون. اقترح أرسطو في وقت لاحق حلاً فلسفيًا للمفارقة، ولكن يبدو أن الجانب الرياضي لم يُحل حتى عالجه أرخميدس. عالج الفيلسوف ديمقريطس، صاحب المبدأ الذري، في ما سبق هذه المسألة، وكان من المتقدمين الذين عاشوا قبل أرسطو. كانت من خلال طريقة استنفاد أرخميدس أنه يمكن إجراء عدد لانهائي من الأقسام الفرعية المستمرة لتحقيق نتيجة منتهية.[3] استخدم الرياضياتي الصيني ليو هوي بشكل مستقل طريقة مماثلة بعد بضعة قرون.[4]
أعطى مادهافا من سانغماغراما في القرن الرابع عشر أقدم الأمثلة على متسلسلة تايلور المحددة (ولكن ليس الطريقة العامة).[5] على الرغم من عدم وجود أي سجل لأعماله، إلا أن كتابات أتباعه في مدرسة كيرلا لعلم الفلك والرياضيات تشير إلى أنه وجد متسلسلات تايلور للدوال المثلثية: الجيب وجيب التمام وقوس الظل (طالع متسلسلات مادهافا). خلال القرنين التاليين، ثم طور أتباعه المزيد من مفكوكات المتسلسلة والتقريبات بالدوال الكسرية.
عرض جيمس غريغوري في رسالته إلى جون كولينز في أواخر عام 1670م، العديد من متسلسلات ماكلورين (sin x، وcos x، وarcsin x، وx cot x) المشتقة من قبل إسحاق نيوتن، وأخبر أن نيوتن قد طور طريقة عامة لنشر الدوال في شكل متسلسلات. في الواقع، استخدم نيوتن طريقة مرهقة تنطوي على تقسيم طويل للمتسلسلة والتكامل حدًّا تلو الآخر، لكن غريغوري لم يكن يعرف ذلك وشرع في اكتشاف طريقة عامة لنفسه. في أوائل عام 1671، اكتشف غريغوري شيئًا مثل متسلسلة ماكلورين العامة وأرسل رسالة إلى كولينز تتضمن المتسلسلات الخاصة بـ (قوس الظل)، و (ظل الزاوية)، و (قاطع الزاوية)، و (اللوغاريتم الطبيعي لقاطع x، وهو تكامل دالة الظل)، و (تكامل دالة القاطع [English]، وهي الدالة العكسية للدالة الغودرمانية)، و (قوس قاطع الجذر التربيعي للعدد 2 مضروب في الدالة الأسية)، و (الدالة الغودرمانية). ومع ذلك، معتقدًا أنه قد أعاد تطوير طريقة نيوتن، لم يصف غريغوري أبدًا كيف حصل على هذه المتسلسلة، ولا يمكن الاستدلال إلا على أنه فهم الطريقة العامة من خلال فحص الأعمال الأولى التي كتبها على الوجه الخلفي من رسالة أخرى أُرخت سنة 1671م.[6]
كتب إسحاق نيوتن بين عامي 1691 و1692م، بيانًا صريحًا لمتسلسلات تايلور وماكلورين في نسخة غير منشورة من عملهِ (باللاتينية: De Quadratura Curvarum) (تعني حرفيًّا "عن تربيع المنحنيات"). لكن هذا العمل لم يكتمل أبداً وحذفت الأقسام ذات الصلة من الأجزاء المنشورة عام 1704م، تحت عنوان (باللاتينية: Tractatus de Quadratura Curvarum) (تعني حرفيًّا "أطروحة تربيع المنحنيات").[fr 1]
لم تُنشر طريقة عامة لتوليد هذه المتسلسلة لجميع الدوال التي وضع بروك تايلور متسلسلاتها حتى عام 1715م،[7] وسُميت المتسلسلة بعد ذلك باسم هذا العالم.
سُميت متسلسلة ماكلورين على اسم كولين ماكلورين، وهو أستاذ جامعي في إدنبرة نشر الحالة الخاصة لنتائج تايلور في منتصف القرن الثامن عشر.[8]
الدوال التحليلية
إذا عُبِّر عن f (x) باستعمال متسلسلة قوى متقاربة في قرص مفتوح متمركز عند b في المستوي المركب (أو فترة في مستقيم الأعداد الحقيقية)، يُقال عنها أنها تحليلية في هذه المنطقة. وبالتالي، بالنسبة إلى x في هذه المنطقة، تُعطى f بمتسلسلة قوى متقاربة التالية:[9]
بالاشتقاق بالنسبة لـ x للصيغة أعلاه n مرات، ثم وضع x = b، نحصل على:
تكتب متسلسلة القوى على هذا الشكل:
لما ، تصبح
نشتق الدالة المعطاة، تصبح:
عند تعويض المتسلسلة الأخيرة بـ 0، نحصل على:
ثم نشتق الدالة المشتقة، تصبح:
عند تعويض المشتقة من الدرجة الثانية بـ 0، نحصل على
إذن،
تُستنتج دالة تايلور بتكرار العملية نفسها وبتعويض نسب مشتقات من مختلف الرتب إلى معاملات الخاصة بالدالة الأخيرة.
تتوافق متسلسلة القوى مع متسلسلة تايلور. أي أن الدالة تكون تحليلية في قرص مفتوح متمركز عند b إذا وفقط إذا كانت متسلسلة تايلور الخاصة بها تتقارب نحو قيمة الدالة عند كل نقطة من القرص.
إذا كانت f (x) مساوية لمجموع متسلسلة تايلور الخاصة بها من أجل كل x في المستوي المركب، فإنها تسمى دالة صحيحة. تعد كثيرات الحدود، والدالة الأسية ex، ودالتا الجيب وجيب التمام المثلثيتان، أمثلةً على الدوال الصحيحة. تتضمن أمثلة الدوال غير الصحيحة الجذر التربيعي، واللوغاريتم، والدالة المثلثية الظل ودالتها العكسية قوس الظل. بالنسبة لهذه الدوال، لا تتقارب متسلسلة تايلور إذا كانت x بعيدة عن b.[عر 6][10] أي أن متسلسلة تايلور تتباعد عند x إذا كانت المسافة بين x وb أكبر من نصف قطر التقارب.[10] يمكن استخدام متسلسلة تايلور لحساب قيمة دالة صحيحة في كل نقطة، إذا كانت قيمة الدالة وجميع مشتقاتها معلومة عند نقطة واحدة. تشمل استخدامات متسلسلة تايلور للدوال التحليلية ما يلي:
- يمكن استخدام المجاميع الجزئية (كثيرات الحدود لتايلور) للمتسلسلة تقريبًا للدالة. هذه التقريبات جيدة إذا ضُمِّنت عدد كافٍ من الحدود.
- يمكن إجراء تفاضل وتكامل متسلسلات القوى حدًّا تلو الآخر، وبالتالي فهي سهلة بشكل خاص.[11]
- تُمَدَّد دالة تحليلية بشكل فريد إلى دالة هولومورفية على قرص مفتوح في المستوي المركب. هذا يجعل آلية التحليل المركب متاحة.[12]
- يمكن استخدام المتسلسلة (المدورة) لحساب قيم الدوال عدديًا[13] (غالبًا عن طريق إعادة صياغة كثير الحدود في شكل تشيبيشيف وتقييمها باستخدام خوارزمية كلنشو).[14]
- يمكن إجراء العمليات الجبرية بسهولة على تمثيل متسلسلة القوى؛ على سبيل المثال، تُسْتَنْتَج صيغة أويلر من مفكوكات تايلور للدوال المثلثية والأسية.[15] هذه النتيجة ذات أهمية أساسية في مجالات مثل التحليل التوافقي.
- يمكن للتقريب باستخدام الحدود القليلة الأولى من متسلسلة تايلور أن يجعل للمسائل غير القابلة للحل يمكن حلها في مجال مقصّر؛ غالبًا ما يستخدم هذا التقريب في الفيزياء.
خطأ التقريب والتقارب



توضح الصورة المقابلة تقريب دقيق لدالة الجيب حول النقطة x = 0. المنحنى الوردي هو كثير الحدود من الدرجة السابعة:
الخطأ في هذا التقريب لا يزيد عن |x|9 / 9!. لدورة كاملة متمركزة في نقطة الأصل (−π < x < π)، يكون الخطأ أقل من 0.08215. بشكل خاص، بالنسبة لـ −1 < x < 1، يكون الخطأ أقل من 0.000003.
في المقابل، تظهر أيضًا صورة لدالة اللوغاريتم الطبيعي ln(1 + x) وبعض كثيرات الحدود لتايلور حول a = 0. تتقارب هذه التقريبات نحو الدالة فقط في المنطقة −1 < x ≤ 1؛ خارج هذه المنطقة، تعد كثيرات حدود لتايلور ذات الدرجة الأعلى تقريبات سيئة للدالة.
يُطلق على الخطأ الذي حصل في تقريب دالة بكثير الحدود لتايلور من الدرجة n اسم "الباقي" ويُشار إليه بالدالة Rn(x). يمكن استخدام مبرهنة تايلور للحصول على تقييد لحجم الباقي.[16]
متسلسلة تايلور ليست متقاربة على الإطلاق. إن مجموعة الدوال المُعرَّفة بمتسلسلات تايلور المتقاربة هي في الواقع مجموعة هزيلة في فضاء فريشيه للدوال الملساء.[17] وحتى إذا تقاربت متسلسلة تايلور للدالة f، فلا يلزم أن تكون نهايتها مساوية لقيمة الدالة f (x). فعلى سبيل المثال، الدالة التالية:
هي دالة قابلة للاشتقاق لانهائيَّا عند x = 0، وله جميع المشتقات تساوي الصفر. وبالتالي، فإن متسلسلة تايلور الخاصة بـ f (x) عند x = 0 تساوي صفرًا بشكل مطابق. ومع ذلك، فإن f (x) ليست دالة صفرية، لذلك لا تساوي متسلسلة تايلور الخاصة بها عند نقطة الأصل. وبالتالي، فإن f (x) هي مثال على دوال ملساء غير تحليلية.
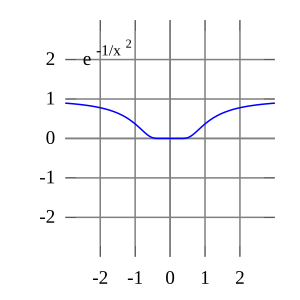
يُظهر مثال في التحليل الحقيقي هذا وجود دوال قابلة للتفاضل لانهائيّا f (x) متسلسلة تايلور الخاصة بها لا تساوي f (x) حتى لو كانت متقاربة. على النقيض من ذلك، فإن الدوال الهولومورفية التي دُرِست في التحليل المركب تمتلك دائمًا متسلسلة تايلور متقاربة، وحتى متسلسلة تايلور للدوال الميرومورفية، والتي قد يكون لها نقاط شاذة، لا تتقارب أبدًا مع قيمة مختلفة عن الدالة نفسها. ومع ذلك، فإن الدالة المركبة e−1/z2 لا تقترب من 0 عندما تقترب z من 0 على طول المحور التخيلي، لذلك فهي ليست مستمرة في المستوي المركب ومتسلسلة تايلور الخاصة بها غير معرفة عند 0.
يمكن أن تظهر كل متتالية الأعداد الحقيقية أو المركبة معاملاتٍ في سلسلة تايلور لدالة قابلة للتفاضل لانهائيًّا معرفة على المستقيم الحقيقي، نتيجة لتوطئة بوريل. نتيجة لذلك، يمكن أن يكون نصف قطر تقارب متسلسلة تايلور يساوي الصفر. حتى أن هناك دوال قابلة للتفاضل لانهائيًا معرفة على المستقيم الحقيقي التي متسلسلات تايلور الخاصة بالدوال لها نصف قطر تقارب يساوي 0 في كل مكان.[18]
لا يمكن كتابة الدالة على شكل متسلسلة تايلور تتمركز على النقطة الشاذة؛ في هذه الحالات، يمكننا في كثير من الأحيان تحقيق متسلسلة إذا سمحنا أيضًا القوى السالبة للمتغير x؛ طالع متسلسلة لوران. على سبيل المثال، يمكن كتابة f (x) = e−1/x2 على شكل متسلسلة لوران.[19]
التعميم
يوجد تعميم لمتسلسلة تايلور يتقارب مع قيمة الدالة نفسها إذا كانت مستمرة محدودة في المجال (0,∞)، يمكن حسابه باستخدام حساب الفروق المحدودة.[20][21] وفقاً للمبرهنة التالية، التي وضعها إينار هيل، من أجل t > 0:
هنا Δn
h هو مؤثر الفرق المنتهي من الرتبة n ذو حجم الخطوة h. المتسلسلة هي بالضبط متسلسلة تايلور، باستثناء أن الفروق المقسَّمة تظهر بدلاً من التفاضل. عندما تكون الدالة f تحليلية عند a، فإن الحدود في المتسلسلة تتقارب نحو حدود متسلسلة تايلور، وبهذا المعنى تعمم متسلسلة تايلور المألوفة.
قائمة متسلسلات ماكلورين لبعض الدوال الشائعة
هذه القائمة للعديد من متسلسلات ماكلورين الهامة. كل هذه المفكوكات صالحة للمداخل المركبة x:
الدالة الأسية
للأساس e لها متسلسلة ماكلورين التالية:[22]

- .
تتقارب من أجل كل x.
الدالة المولدة الأسية لأعداد بيل هي الدالة الأسية لسلف الدالة الأسية:[23]
اللوغاريتم الطبيعي
دالة اللوغاريتم الطبيعي (للأساس e) لها متسلسلة ماكلورين التالية:[24]
تتقارب تلك المتسلسلات من أجل . (بالإضافة إلى ذلك، المتسلسلة الخاصة بـ ln(1 − x) تتقارب من أجل x = −1، والمتسلسلة الخاصة بـ ln(1 + x) تتقارب من أجل x = 1.)
المتسلسلات الهندسية
المتسلسلات الهندسية ومشتقاتها لها متسلسلات ماكلورين التالية:[25]
كلها تتقارب من أجل . هذه حالات خاصة من متسلسلة ثنائي الحد الواردة في القسم التالي.
متسلسلة ثنائي الحد
متسلسلة ثنائي الحد هي متسلسلة القوى التالية:[26]
معاملاتها هي معاملات ثنائي الحد المعممة:[27] (إذا كان n = 0، هذا الجداء هو جداء خالٍ وله قيمة 1.) كلها تتقارب من أجل من أجل كل عدد حقيقي أو مركب α. لما α = −1، فهذه هي في الأساس المتسلسلة الهندسية اللانهائية المذكورة في القسم السابق. تعطي الحالات الخاصة α = 12 و α = −12 دالة الجذر التربيعي ومقلوبها:[25]عندما يُحتفظ بالحد الخطي فقط، فإن هذا يبسط تقريب ثنائي الحد.
الدوال المثلثية
الدوال المثلثية المألوفة ودوالها العكسية لها متسلسلة ماكلورين التالية:[28]
كل الزوايا معبرة عنها بالتقدير الدائري. الأعداد Bk الظاهرة في مفكوكات دالة الظل هي أعداد برنولي. الأعداد Ek الظاهرة في مفكوك دالة القاطع هي أعداد أويلر.
الدوال الزائدية
الدوال الزائدية لها متسلسلة ماكلورين وثيقة الصلة بمتسلسلات الدوال المثلثية السالف ذكرها:[29]
الأعداد Bk الظاهرة في متسلسلة دالة الظل الزائدي هي أعداد برنولي.
دوال متعددة اللوغاريتمات
الدوال المتعددة اللوغاريتمات لها هذه المتطابقات المعرِّفة لها:[30]
دالتا خي للوجندر [English] معرفة على النحو التالي:[31]
والصيغة الواردة أدناه تسمى تكامل دالة الظل العكسية:[31]
هذه الصيغ لها أهمية كبيرة في الديناميكا الحرارية الإحصائية.
الدوال الإهليلجية
يمكن تعريف التكاملين الإهليلجيين التامين من النوع الأول K ومن النوع الثاني E على النحو التالي:[32]
حساب متسلسلات تايلور
توجد طرائق عديدة لحساب متسلسلة تايلور لعدد كبير من الدوال. يمكن محاولة استخدام تعريف متسلسلة تايلور، مع أن هذا يتطلب غالبًا تعميم شكل المعامِلات وفقًا لنمط واضح بسهولة. بدلاً من ذلك، يمكن استخدام العمليات مثل التعويض أو الضرب أو القسمة أو الجمع أو الطرح لمتسلسلة تايلور القياسية لإنشاء متسلسلة تايلور لدالة، بحكم أن متسلسلة تايلور هي متسلسلة قوى.[33] في بعض الحالات، يمكن أيضًا اشتقاق متسلسلة تايلور من خلال تطبيق مكاملة بالتجزئة بشكل متكرر. من الملائم بشكل خاص استخدام أنظمة الجبر الحاسوبية لحساب متسلسلة تايلور.
المثال الأول
المطلوب حساب كثير الحدود لماكلورين من الدرجة السابعة للدالة التالية:
- ،
يمكن أولاً إعادة كتابة الدالة على الشكل التالي:
متسلسلة تايلور للوغاريتم الطبيعي هي (باستخدام تدوين O الكبير):[34]
بالنسبة لدالة جيب التمام:
للمتسلسلة الأخيرة حد ثابت مساوٍ للصفر، أي يمكن تعويض المتسلسلة الثانية في الأولى وإزالة الحدود ذات الدرجة الأعلى من الدرجة السابعة بسهولة باستخدام تدوين O الكبير:
لأن جيب التمام دالة زوجية، بلزم أن تكون معاملات القوى الفردية كلها، أي x، x3، x5، x7، ... مساوية للصفر.
المثال الثاني
المطلوب إيجاد متسلسلة تايلور عند النقطة 0 للدالة:
بالنسبة للدالة الأسية:
وكما في المثال الأول:
متسلسلة القوى، افتراضاً، هي:
يكون الناتج عندئذ، بعد ضرب المقام وبتعويض سلسلة جيب التمام:
بجمع الحدود حتى الحد ذي الدرجة الرابعة:
يمكن إيجاد قيم من خلال مطابقة المعاملات مع متسلسلة ، وينتج عنها:
المثال الثالث
ستُستخدم طريقة تسمى "النشر غير المباشر"، أو "الفك غير المباشر"، لنشر الدالة المعطاة. تُستخدم هذه الطريقة نشر تايلور المعروفة للدالة الأسية. من أجل نشر (1 + x)ex على سبيل المثال على شكل متسلسلة تايلور بدلالة x، نستخدم متسلسلة تايلور المعروفة لدالة ex على سبيل المثال:
وبالتالي،
متسلسلات تايلور تعريفاتٍ
تُعَرَّف الدوال الجبرية بمعادلة جبرية، وتُعَرَّف الدوال المتسامية (بما في ذلك تلك التي تمت مناقشتها أعلاه) ببعض الخصائص التي تحملها، مثل المعادلة التفاضلية.[35] على سبيل المثال، الدالة الأسية هي الدالة التي يساوي مشتقها نفسه دائمًا، وتفرض قيمة 1 عند الأصل. يمكن مع ذلك تعريف دالة تحليلية تعريفاً وافياً باستعمال بمتسلسلة تايلور الخاصة بها.
تُستخدم متسلسلة تايلور لتعريف الدوال و"المؤثرات" في ميادين متنوعة من الرياضيات. على وجه الخصوص، هذا صحيح في الميادين التي تتعطل فيها التعريفات التقليدية للدوال. على سبيل المثال، باستخدام متسلسلة تايلور، يمكن أن يمدد الدوال التحليلية إلى مجموعات من المصفوفات والمؤثرات، مثل الدالة الأسية لمصفوفة [English] أو لوغاريتم مصفوفة [English].[36]
يكون من الأنسب العمل مباشرةً مع متسلسلة القوى نفسها في الميادين أخرى، مثل التحليل الشكلي.[ملاحظة 1] وهكذا يمكن تعريف حل معادلة تفاضلية على أنه متسلسلة قوى، والتي نأمل أن نثبت أنها متسلسلة تايلور للحل المطلوب.
متسلسلة تايلور لدالة متعددة المتغيرات
يمكن أيضًا تعميم متسلسلة تايلور على دالة ذات أكثر من متغير باستخدام:[37][38]
على سبيل المثال، بالنسبة للدالة التي تعتمد على متغيرين x و y، متسلسلة تايلور إلى غاية الدرجة الثانية حول النقطة (a, b) هي:
حيث تشير الأدلة السفلية إلى المشتقات الجزئية للدالة.
متسلسلة تايلور من الدرجة الثانية لدالة متعددة المتغيرات
يمكن كتابة متسلسلة تايلور من الدرجة الثانية لدالة ذات قيمة سُلَّمية لأكثر من متغير بإحكام:[39]
حيث D f (a) هو تدرج f مُقيّمة عند x = a و D2 f (a) هي مصفوفة هيسية. بتطبيق التدوين المتعدد الأدلة، تصبح متسلسلة تايلور لمتعدد المتغيرات:
والتي يجب أن تُفهم على أنها نسخة متعددة الأدلة أكثر اختصارًا للمعادلة الأولى لهذه الفقرة، مع تشابه تام مع متسلسلة الدالة وحيدة المتغير.
المثال
من أجل حساب متسلسلة تايلور من الدرجة الثانية حول النقطة (a, b) = (0, 0) للدالة:

نحسب أولاً جميع المشتقات الجزئية الضرورية:
يعطي تقييم هذه المشتقات عند الأصل معاملات تايلور التالية:
تعويض هذه القيم بالصيغة العامة:
تنتج:
بما أن ln(1 + y) تحليلية عند |y| < 1، لدينا:
المقارنة بمتسلسلة فورييه
تُمكِّن متسلسلة فورييه المثلثية من التعبير عن دالة دورية (أو دالة معرفة على فترة مغلقة [a,b]) على شكل مجموع لانهائي من الدوال المثلثية (الجيب وجيب التمام). وبهذا المعنى، فإن متسلسلة فورييه مماثلة لمتسلسلة تايلور، لأن الأخيرة تسمح بتعبير عن دالة مجموعًا لانهائيًّأ من الأسس. ومع ذلك، تختلف المتسلسلتان عن بعضهما البعض في العديد من القضايا ذات الصلة:
- التدويرات المحدودة لمتسلسلة تايلور للدالة f (x) حول النقطة x = a كلها تساوي تمامًا f عند a. على النقيض من ذلك، تُحسب متسلسلة فورييه بمكاملة على فترة كاملة، لذلك لا توجد عمومًا أية نقطة حيث تكون جميع التدويرات المحدودة للمتسلسلة دقيقة.[40]
- يتطلب حساب متسلسلة تايلور معرفة الدالة في جوار صغير اختياري من نقطة، في حين أن حساب متسلسلة فورييه يتطلب معرفة الدالة في كامل مجالها. بمعنى ما يمكن القول أن متسلسلة تايلور "محلية" ومتسلسلة فورييه "عامة".[41]
- تُعَرَّف متسلسلة تايلور لدالة لها العديد من المشتقات اللانهائية عند نقطة واحدة، بينما تُعَرَّف متسلسلة فورييه لأي دالة قابلة للتكامل. على وجه الخصوص، لا يمكن أن تكون الدالة دائمًا قابلة للاشتقاق في أي مكان. (على سبيل المثال، يمكن أن تكون f (x) دالة فايرشتراس.)[41]
- تقارب كلتا المتسلسلتين له خصائص مختلفة جدًا. حتى إذا كانت متسلسلة تايلور لها نصف قطر تقارب موجب، فقد لا تتوافق المتسلسلة الناتجة مع الدالة؛ ولكن إذا كانت الدالة تحليلية، فإن المتسلسلة تتقارب نقطة بنقطة نحو الدالة، وبشكل منتظم في كل مجموعة جزئية متراصة من فترة التقارب. فيما يتعلق بسلسلة فورييه، إذا كانت الدالة قابلة للتكامل تربيعيا، فإن المتسلسلة تتقارب في متوسط تربيعي، ولكن هناك حاجة إلى متطلبات إضافية لضمان التقارب النقطي أو المنتظم (على سبيل المثال، إذا كانت الدالة دورية ومن الصنف C1، فإن التقارب يكون منتظمًا).[42]
- أخيرًا، من الناحية العملية، يريد الشخص تقريب الدالة بعدد محدود من الحدود، على سبيل المثال بكثير الحدود لتايلور أو مجموع جزئي للمتسلسلة المثلثية، على الترتيب. في حالة متسلسلة تايلور، يكون الخطأ صغيرًا جدًا في جوار النقطة التي يُحسب فيها، في حين أنه قد يكون كبيرًا جدًا في نقطة بعيدة. في حالة متسلسلة فورييه، يتوزع الخطأ على طول مجال الدالة.
ملحق: مسرد المصطلحات الإنجليزية
| مَسرد المفردات وفق الترتيب الأبجدي الإنجليزي | |
| A | |
| جمع | Addition |
| معادلة جبرية | Algebraic equation |
| دالة تحليلية | Analytic function |
| تقريب | Approximation |
| قوس القاطع | Arcsecant |
| مدخل | Argument |
| قوس الظل | Arctangent |
| B | |
| عدد برنولي | Bernoulli number |
| دالة بيسل | Bessel function |
| تدوين O الكبير | Big O notation |
| معاملات ثنائي الحد | Binomial coefficient |
| متسلسلة ثنائي الحد | Binomial series |
| توطئة بوريل | Borel's lemma |
| C | |
| حساب التفاضل والتكامل | Calculus |
| شكل تشيبيشيف | Chebyshev form |
| صنف | Class |
| خوارزمية كلنشو | Clenshaw algorithm |
| معامل | Coefficient |
| مجموعة متراصة | Compact set |
| تكامل إهليلجي تام من النوع الأول/الثاني | Complete elliptic integral of the first/second kind |
| تحليل مركب | Complex analysis |
| دالة مركبة | Complex function |
| عدد مركب | Complex number |
| مستوي مركب | Complex plane |
| دالة ذات قيم مركبة | Complex-valued function |
| نظام الجبر الحاسوبي | Computer algebra system |
| دالة مستمرة | Continuous function |
| متسلسلة متقاربة | Convergent series |
| D | |
| درجة | Degree |
| مقام | Denominator |
| مشتق | Derivative |
| فرق | Difference |
| دالة قابل للاشتقاق/التفاضل | Differentiable function |
| تفاضل | Differential |
| معادلة تفاضلية | Differential equation |
| قرص | Disk |
| متسلسلة متباعدة | Divergent series |
| قسمة | Division |
| مجال دالة | Domain of a function |
| E | |
| دالة صحيحة | Entire function |
| خطأ | Error |
| صيغة أويلر | Euler's formula |
| زوجي | Even (function or number) |
| نشر/فك | Expansion |
| دالة أسية | Exponential function |
| F | |
| عاملي عدد | Factorial of a number |
| فرق محدود | Finite difference |
| التحليل الشكلي | Formal analysis |
| متسلسلة فورييه | Fourier series |
| فضاء فريشيه | Fréchet space |
| G | |
| متسلسلة هندسية | Geometric series |
| تدرج | Gradient |
| تمثيل بياني لدالة | Graph of a function |
| دالة غودرمانية | Gudermannian function |
| H | |
| تحليل توافقي | Harmonic analysis |
| مصفوفة هيسية | Hessian Matrix |
| دالة هولومورفية | Holomorphic function |
| دوال زائدية | Hyperbolic functions |
| ظل زائدي | Hyperbolic tangent |
| I | |
| محور تخيلي | Imaginary axis |
| عدد صحيح | Integer number |
| تكامل | Integral |
| تكامل/مكاملة | Integration |
| تكامل بالتجزئة | Integration by parts |
| فترة | Interval |
| دالة عكسية | Inverse function |
| L | |
| متسلسلة لوران | Laurent series |
| دالة خي للوجندر | Legendre chi function |
| نهاية دالة | Limit of a function |
| مستقيم | Line |
| M | |
| متسلسلة ماكلورين | Maclaurin series |
| مصفوفة | Matrix |
| مجموعة هزيلة | Meagre (meager) set |
| طريقة استنفاد | Method of exhaustion |
| دالة ميرومورفية | Meromorphic function |
| تدوين متعدد الأدلة | Multi-index notation |
| ضرب | Multiplication |
| N | |
| لوغاريتم طبيعي | Natural logarithm |
| جوار | Neighbourhood |
| بسط | Numerator |
| O | |
| فردي | Odd (function or number) |
| نقطة الأصل | Origin |
| عملية | Operation |
| مؤثر | Operator |
| P | |
| مفارقة | Paradox |
| مجموع جزئي | Partial sum |
| تقارب نقطة بنقطة | Pointwise convergence |
| متعدد اللوغاريتمات | Polylogarithm |
| كثير الحدود | Polynomial |
| أس/قوة | Power |
| متسلسلة قوى | Power series |
| حاصل ضرب/جداء | Product |
| Q | |
| تربيع (منحنيات) | Quadrature |
| R | |
| نسبة | Ratio |
| نصف قطر التقارب | Radius of convergence |
| دالة كسرية | Rational function |
| عدد كسري/نسبي/ناطق/جذري | Rational number |
| عدد حقيقي | Real number |
| مقلوب | Reciprocal |
| باق | Remainder |
| جذر معادلة/جذر دالة | Root |
| مُدوَّر | Round/truncated |
| S | |
| سُلَّمي | Scalar |
| قاطع زاوية | Secant of an angle |
| متتالية | Sequence |
| تدوين سيغما | Sigma notation |
| نقطة شاذة | Singularity |
| دالة ملساء | Smooth function |
| دالة مثلثية | Special functions |
| دالة قابل للتكامل تربيعيا | Square-integrable function |
| جذر تربيعي | Square root |
| الديناميكا الحرارية الإحصائية | Statistical thermodynamics |
| مجموعة جزئية | Subset |
| طرح | Subtraction |
| مجموع | Sum |
| T | |
| مماس | Tangent |
| ظل زاوية | Tangent of an angle |
| مبرهنة تايلور | Taylor theorem |
| حد (لمعادلة) | Term |
| دالة متسامية | Transcendental function |
| دالة مثلثية | Trigonometric function |
| متسلسلة مثلثية | Trigonometric series |
| U | |
| تقارب منتظم | Uniform convergence |
| V | |
| متغير | Variable |
| W | |
| دالة فايرشتراس | Weierstrass function |
| Z | |
| مفارقة زينون | Zeno's paradoxes |
انظر أيضًا
| في كومنز صور وملفات عن: متسلسلة تايلور |
الهوامش والملاحظات
- ^ التحليل الشكلي هو دراسة متسلسلة القوى الشكلية، ومتسلسلة لوران الشكلية، ومتسلسلة الجذور الشكلية، وغيرها من المتسلسلات أو الدوال الشكلية.
المراجع
فهرس المراجع
- بالعربية
- ^ دعبول (2018)، ص. 703.
- ^ مكتب التنسيق (1990)، ص. 148.
- ^ يدري (2018)، ص. 153.
- ^ خضيري (2020)، ص. 168.
- ^ يدري (2019)، ص. 315.
- ^ مجمع القاهرة (2000)، ص. 101.
- بالإنكليزية
- ^ أ ب Thomas (1995), p. 673 .
- ^ Lindberg (2007), p. 33 .
- ^ Kline (1990), vol. 2, p. 801 .
- ^ Boyer (1991), p. 202–203 .
- ^ Dani (2012), p. 236–246 .
- ^ [a] Turnbull (1939), p. 168–174 .
[b] Roy (1990), p. 291–306 .
[c] Malet (1993), p. 97–137 .
- ^ [a] Taylor (1715), p. 21–23 (Prop. VII, Thm. 3, Cor. 2) .
[b] Feigenbaum (1985), p. 1-140 .
[c] Struik (1969), p. 329-332 .
- ^ Struik (1969), p. 338 .
- ^ Thomas (1995), p. 667 .
- ^ أ ب Holland (1973), p. 183-184 .
- ^ Thomas (1995), p. 667-668 .
- ^ Holland (1973), p. 182-183 .
- ^ Thomas (1995), p. 682-683 .
- ^ Lee (1970), p. 1-2 .
- ^ Thomas (1995), p. 684 .
- ^ Thomas (1995), p. 679 .
- ^ Buhler (2018), p. 44 .
- ^ Rudin (1980), p. 418 .
- ^ Giaquinta (2010), p. 192 .
- ^ Feller (2003), p. 230–2 .
- ^ Hille (1957), p. 300–327 .
- ^ Abramowitz (1972), p. 69 .
- ^ Wilf (2013), p. 21 .
- ^ Abramowitz (1972), p. 68 .
- ^ أ ب Abramowitz (1972), p. 15 .
- ^ Abramowitz (1972), p. 10-14-15 .
- ^ Abramowitz (1972), p. 10 .
- ^ Abramowitz (1972), p. 74-75, 81 .
- ^ Abramowitz (1972), p. 85 .
- ^ Abramowitz (1972), p. 1004 .
- ^ أ ب Weisstein (2002), p. 136 .
- ^ Abramowitz (1972), p. 591 .
- ^ Thomas (1995), p. 682 .
- ^ Izaac (2019), p. 165 .
- ^ Thomas (1995), p. 529-530 .
- ^ Taylor (2011), p. 146-147 .
- ^ Hormander (2003), p. 5–32 .
- ^ Duistermaat (2010), p. 59-63 .
- ^ Binmore (2001), p. 171 .
- ^ Singh (2006), p. 22-23 .
- ^ أ ب Babu (2014), p. 1-8 .
- ^ Howell (2001), p. 402 .
- بالفرنسية
- ^ Whiteside (1983), p. 186-188 .
معلومات الكاملة المراجع
- الدوريات (مرتبة حسب سنة النشر ثم اسم المؤلف)
- بالإنكليزية
- بالفرنسية
- Q122764742، QID:Q122764742
- الكتب (مرتبة حسب سنة النشر ثم اسم المؤلف)
- بالعربية
- Q114600477، QID:Q114600477
- Q120333812، QID:Q120333812
- Q108593221، QID:Q108593221
- Q122705552، QID:Q122705552
- Q122642210، QID:Q122642210
- بالإنكليزية
- Q42191653، QID:Q42191653
- Q122474906، QID:Q122474906
- Q122443198، QID:Q122443198
- Q122416676، QID:Q122416676
- Q122473416، QID:Q122473416
- Q14917272، QID:Q14917272
- Q110635241، QID:Q110635241
- Q120867638، QID:Q120867638
- Q120969870، QID:Q120969870
- Q122707244، QID:Q122707244
- Q122640444، QID:Q122640444
- Q27102399، QID:Q27102399
- Q122531778، QID:Q122531778
- Q122531113، QID:Q122531113
- Q122648416، QID:Q122648416
- Q122416743، QID:Q122416743
- Q56339851، QID:Q56339851
- Q122609529، QID:Q122609529
- Q122613508، QID:Q122613508
- Q122642097، QID:Q122642097
- Q122609566، QID:Q122609566
- Q122529709، QID:Q122529709
- Q122647976، QID:Q122647976
- اللاتينية
- Q122442633، QID:Q122442633
- التقارير
- بالإنكليزية
- Q122474059، QID:Q122474059
